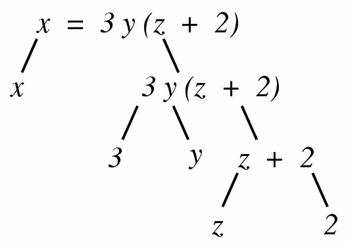|
One of the key features ensuring robustness and re-usability of CellML components and models is the requirement that units be associated with all variables and numbers in a CellML document. This allows components and models that declare variables with different units to be connected, as long as variables that are mapped to one another have the same dimensions. For instance, it is possible to map a variable declared with units of "pound/foot" to a variable declared with units of "kilogram/metre", but not to a variable declared with units of "mole/litre" or "kilogram-squared/metre". The explicit declaration of units also allows CellML processing software to check the consistency of each equation in a model.
CellML provides a dictionary of standard units that may be used in variable declarations or attached to bare numbers in mathematics. References to these units should make use of the actual name of the units, rather than the standard abbreviation, thus avoiding confusion between units (e.g., metre) and prefixes (e.g., milli). The full list of units that any CellML processing application is expected to recognise is given in Table 2. The keywords in the table comprise the SI base and derived units and some additional units commonly used in the types of biological models likely to be defined using CellML. Expressions relating these additional units to the SI base units are provided in Section 5.2.2. The only unfamiliar name on this list is dimensionless, which is used to indicate that a number or variable has no units associated with it.
| ampere | |
farad | |
katal | |
lux | |
pascal | |
tesla |
| becquerel | |
gram | |
kelvin | |
meter | |
radian | |
volt |
| candela | |
gray | |
kilogram | |
metre | |
second | |
watt |
| celsius | |
henry | |
liter | |
mole | |
siemen | |
weber |
| coulomb | |
hertz | |
litre | |
newton | |
sievert | |
|
| dimensionless | |
joule | |
lumen | |
ohm | |
steradian | |
|
Table 2
The dictionary of units keywords that CellML processing applications are expected to recognise. Base SI units are printed in bold text, derived SI units are printed in plain text, and additions to the standard units defined purely for the convenience of model authors are italicised.
This list is based on the ISO standard, including the year 2000 supplement. The American spellings of "meter" and "liter" are taken from the NIST Guide for the Use of the International System of UNITS (SI). The ISO standard defines the mathematical relationships between the derived SI units and the base SI units.
The CellML <units> elements in Figure 7 define the non-SI units in Table 2 (the italicised keywords) in terms of SI units. The format of the units element is formally specified in Section 5.2.3.
<!--
x_new [celsius] = 1.0 [celsius/kelvin] x_old [kelvin] - 273.15 [celsius]
-->
<units name="celsius">
<unit offset="-273.15" units="kelvin" />
</units>
<!--
"dimensionless" is used for numbers that do not have units.
-->
<units name="dimensionless" />
<!--
x_new [gram] = 0.001 [gram/kilogram] x_old [kilogram]
-->
<units name="gram">
<unit multiplier="0.001" units="kilogram" />
</units>
<!--
x_new [litre] = 1000 [litre/metre^3] (centi)^3 x_old [metre^3]
-->
<units name="litre">
<unit multiplier="1000" prefix="centi" units="metre" exponent="3" />
</units>
Figure 7
These <units> elements define the non-SI units included in the standard CellML units dictionary in terms of SI units. The definition of liter is exactly the same as the definition of litre, and is therefore omitted. Note that these definitions must not be used in CellML documents: model authors are forbidden from defining units with the same names as those in the standard dictionary in Table 2.
CellML also provides a facility whereby new units can be defined in terms of the units provided in the dictionary. This functionality allows the definition of units which are expressed as a scaled version of other units (as is the case for most imperial units), the definition of units which are made up of the product of other units, and even the creation of units that require an offset, such as degrees Fahrenheit. This allows model authors to work in whatever set of units they feel most comfortable, while still ensuring that their models can be integrated with those of other authors using other units.
New units are defined using the <units> element, which may be placed inside both <model> and <component> elements. When a <units> element is placed inside the <model> element, the units definition may be referenced from within any component in the model. When a <units> element is placed inside a <component> element, the units definition may only be referenced from within that component.
Each units element must define a name attribute, which is used to reference the units definition elsewhere. The value of the name attribute must be unique across all <units> elements in the <model> or <component> element in which it is defined. If the value of the name attribute of a <units> element defined inside a <component> element matches the value of the name attribute on a <units> element defined inside the parent <model> element, then it will redefine the units, and all references to these units within the component element refer to the new definition. Model authors must not redefine any of the standard units. Therefore, the value of the name attribute must not equal one of the names from the standard units dictionary in Table 2.
A <units> element may also define a base_units attribute, the associated behaviour of which is discussed in Section 5.2.4. A <units> element can contain a set of <unit> elements that reference units from the dictionary or some previously defined units.
A <unit> element has no content but may have up to five attributes. The units attribute is the only one that is required. It is used to set the base quantity for the current <unit> element, and its value must correspond to a keyword from the standard CellML units dictionary or to the value of the name attribute of a <units> element in the current component or model.
The definition of new units in terms of subunits may require the use of some combination of the optional offset, prefix, exponent, and multiplier attributes.
A multiplier attribute can be used to pre-multiply the quantity to be converted by any real scale factor. For instance, a multiplier of 0.45359237 is used to define a pound in terms of a kilogram. The multiplier attribute has a default value of "1.0"
The offset attribute is used to represent the addition of a constant in the transformation between the current units and the base units. This should only be necessary for the definition of temperature scales. For instance, an offset attribute value of "32.0" is needed to define Fahrenheit in terms of Celsius. The offset attribute has a default value of "0.0".
The prefix attribute can be used to indicate a scale for the referenced units. It is included primarily for the convenience of modellers who want to define units that differ from another units definition only by an SI scale factor. Its value must be from the standard set of CellML prefix names given in Table 3 or be an integer, in which case the units are pre-multiplied by 10 to the power of this number. The default value of the prefix attribute is "0.0", (the referenced units are scaled by a factor of one).
| name |
factor |
symbol |
name |
factor |
symbol |
| yotta |
1024 |
Y |
deci |
10-1 |
d |
| zetta |
1021 |
Z |
centi |
10-2 |
c |
| exa |
1018 |
E |
milli |
10-3 |
m |
| peta |
1015 |
P |
micro |
10-6 |
u |
| tera |
1012 |
T |
nano |
10-9 |
n |
| giga |
109 |
G |
pico |
10-12 |
p |
| mega |
106 |
M |
femto |
10-15 |
f |
| kilo |
103 |
k |
atto |
10-18 |
a |
| hecto |
102 |
h |
zepto |
10-21 |
z |
| deka |
101 |
da |
yocto |
10-24 |
y |
Table 3
The set of names that may be used in the prefix attribute on a <unit> element and the corresponding scale factors that will pre-multiply the unit. The standard abbreviation for each unit is provided for reference, but must not be used in the prefix attribute.
The scale factor described by the prefix attribute and the units referenced by the units attribute are raised to a power equal to the value of the exponent attribute. The value of the exponent attribute must be a floating point number, and is typically an integer. The exponent attribute has a default value of "1.0". Note that an exponent attribute value of "0.0" has the effect of removing the parent <unit> element from the current units definition.
A `simple units' definition occurs when units are defined as a linear function of some previously defined simple units or base units. This occurs when a <units> element contains only a single child <unit> element, that <unit> element has an exponent attribute value of "1.0", and the units definition referenced by the units attribute is one of the SI or user-defined base units or is itself a simple units definition. These are the only conditions under which a <unit> element may define an offset attribute. The formula that expresses how the old units (referenced by the value of the units attribute on the <unit> element) are transformed into the new units (defined by the value of the name attribute on the parent <units> element) is given below:
xnew[ Units ] = ( multiplier [ Units/units ] prefix ) xold [ units ] + offset [ Units ] (1)
Terms in square brackets represent the units associated with a term in the expression, xold is the value to be transformed from the old units, xnew is the resulting value in the new units, Units are the units being defined, and multiplier, prefix, units, and offset correspond to the values of the appropriate attributes on the <unit> element.
`Complex units' are the product of multiple base quantities, and are created by placing several <unit> elements inside a single <units> element, or by defining an exponent attribute with a value other than "1.0" on any <unit> element. The conversion between the new units and the product of the constituent units is given by the formula below:
xnew [ Units ] = xold [ u1e1 ... unen ] m1 [ Units1/n / u1e1 ] p1e1 ... mn [ Units1/n / unen ] pnen (2)
The mn, pn, un, and en terms refer to the values of the multiplier, prefix, units, and exponent attributes on the n-th <unit> element respectively. Note that this specification forbids offset attributes from being defined on any unit elements that occur inside a complex units definition.
It is very important to note that when a complex units definition references a simple units definition, any offset associated with the simple units definition is removed. This means that the conversions such as the one between degrees Fahrenheit per inch and degrees Celsius per centimetre involve only a scale factor.
A modeller might want to define and use units for which no simple conversion to SI units exist. A good example of this is pH, which is dimensionless, but uses a log scale. Ideally, pH should not simply be defined as dimensionless because software might then attempt to map variables defined with units of pH to any other dimensionless variables.
CellML addresses this by allowing the model author to indicate that a units definition is a new type of base unit, the definition of which can not be resolved into simpler subunits. This is done by defining a base_units attribute value of "yes" on the <units> element. This element must then be left empty. The base_units attribute is optional and has a default value of "no". If the base_units attribute is omitted or assigned a value of "no", units are expected to be defined in terms of other units as described in Section 5.2.3.
The indiscriminate use of the base_units attribute is strongly discouraged, because it has a significant impact on the re-usability of models and components. In particular, the base_units attribute should not be used to restrict users to creating models with an application-specific dictionary of units, as this prevents the efficient exchange of CellML models with other applications.
Software that is checking the consistency of the units in an equation (described in more detail in Section 5.2.5) can stop the recursive resolution of units definitions when the only remaining units are base SI units and user-defined base units.
The association of units with every variable and bare number that appears in an equation in a CellML document provides CellML processing software the opportunity to perform equation dimension checking. Verifying that equations have consistent dimensions can potentially catch many basic mathematical errors. CellML Level One conformant software is free to ignore units in mathematics and assume that equations are consistent. CellML Level Two conformant software must check the consistency of dimensions in equations.
Section 5.5.5 specifies a possible implementation of equation dimensionality checking. This implementation splits an equation into a tree of equation parts, in which each parent part if obtained by the application of a single operator to its children. The units definition on each leaf node (i.e., part without children) is expanded into base units, as described in Section 5.5.4. The units definition for a node at a higher level of the tree is constructed by combining the units definition of its children. An equation has consistent dimensions if the fully expanded units definitions of the two nodes at the top level of the tree are equivalent, as defined in Section 5.5.3.
This specification does not require software to use the implementation discussed in Section 5.5.5, but does require that software that claims to perform dimension checking achieve the same results as if that implementation were used.
This specification does not attempt to completely prevent model authors from creating bad mathematics. Dimension consistency checking prevents modellers from adding variables with different dimensions but would not find errors in the following equations, which have different units but the same dimensions:
(x volts) = (y volts) + (z millivolts)
(x inches) = (y metres) + (z nautical_miles)
Although it would be technically possible to find and correct such errors, CellML processing software is not required to be able to do so.
Associating units definitions with every variable declaration in a component allows variables from components that make use of different sets of units to be mapped together, as long as the variables have the same dimensions. Section 5.5.6 specifies a possible implementation of the conversion of a numeric value from one set of units to another. This specification does not require that software use this implementation but does require that software that claims to support units conversion during variable mapping achieve the same results as if this implementation were used.
This implementation generates an expression that relates each units definition to SI and user-defined base units. This expression is obtained by recursively expanding each units definition as described in Section 5.5.4, and then simplifying the result. The expression for the input units is then inverted to give an expression that relates the appropriate base units to the input units. This inverted expression is substituted into the expression for the target units, producing a single expression that relates the quantity to be converted from the input units to a corresponding quantity in the target units. The inversion and substitution process is described in Section 5.5.7.
Figure 8 shows several CellML units definitions, demonstrating how simple units can be expressed as linear functions of other simple units, and how complex units are obtained from the product of other units.
<!--
Simple Units Definition 1
x_new [fahrenheit] = 1.8 [fahrenheit/celsius] x_old [celsius] + 32.0 [fahrenheit]
-->
<units name="fahrenheit">
<unit multiplier="1.8" offset="32.0" units="celsius" />
</units>
<!--
Simple Units Definition 2
x_new [rankine] = 1.8 [rankine/kelvin] x_old [kelvin]
-->
<units name="rankine">
<unit multiplier="1.8" units="kelvin" />
</units>
<!--
Simple Units Definition 2
x_new [inch] = 2.54 [inch/metre] centi x_old [metre]
-->
<units name="inch">
<unit multiplier="2.54" prefix="centi" units="metre" />
</units>
<!--
Complex Units Definition 1
x_new [millimolar] = milli x_old [ mole ( litre )^-1 ]
-->
<units name="millimolar">
<unit prefix="milli" units="mole" />
<unit units="litre" exponent="-1" />
</units>
<!--
Complex Units Definition 2
x_new [fahrenheit_per_inch] = x_old [ fahrenheit (inch)^-1 ]
-->
<units name="fahrenheit_per_inch">
<unit units="fahrenheit" />
<unit units="inch" exponent="-1" />
</units>
<!--
Complex Units Definition 3
x_new [celsius_per_centimetre] = x_old [ celsius (metre)^-1 ] (centi)^-1
-->
<units name="celsius_per_centimetre">
<unit units="celsius" />
<unit prefix="centi" units="metre" exponent="-1" />
</units>
Figure 8
Some examples of the use of the <units> element demonstrating the definition of simple and complex units.
The first step in the algorithm proposed in Section 5.5.5 for verifying that a given equation has consistent dimensions is to convert the equation into a tree of equation parts. A relational operator (typically the equals operator) combines the nodes at the top of the tree. For instance, the equation:
would have the tree shown in Figure 9.
Figure 9
The tree form of the equation x = 3y(z + 2), in which each non-leaf node is obtained by the application of a single operator to its children.
Units are a fundamental part of a CellML model definition. In this section, formal rules are specified for the system of units definition introduced in Section 5.2.
- Allowed use of the
<units> element
-
Both the <model> and <component> elements can contain any number of <units> elements.
-
Each <units> element must define a name attribute, and may define a base_units attribute.
-
If a <units> element defines a base_units attribute with a value of "yes", then that <units> element must contain only the following elements,
which may appear in any order:
- metadata framework elements, as described in Section 8.
-
If a <units> element does not define a base_units attribute with a value of "yes", then that <units> element must contain only the following elements,
which may appear in any order:.
<unit> elements in the CellML namespace,- metadata framework elements, as described in Section 8.
- Allowed values of the
name attribute
-
The value of the name attribute must be a valid CellML identifier as discussed in Section 2.2.1.
-
The value of the name attribute must not equal one of the names defined in the standard dictionary of units in Table 2.
[ Model authors may not redefine the standard units. ]
-
The value of the name attribute must be unique across all <units> elements at the same level in a CellML document.
[ Two <units> elements in the same <model> element may not have the same name attribute value, although a <units> element in a <component> element may share the same name as a <units> element in the parent <model> element. In this case, the units definition in the <component> element supercedes the model-wide definition when referenced inside that component. ]
- Allowed values of the
base_units attribute
-
If present, the value of the base_units attribute must be "yes" or "no".
-
If not present, the value of the base_units attribute defaults to "no".
- Allowed use of the
<unit> element
-
A <unit> element must contain only the following elements,
which may appear in any order:
- metadata framework elements, as described in Section 8.
-
Each <unit> element must define a units attribute. It may also define prefix, exponent, multiplier, and offset attributes.
- Allowed values of the
units attribute
-
The value of the units attribute must be taken from the standard dictionary of units listed in Table 2 or be the value of the name attribute on a <units> element defined in the current <component> or <model> element.
-
The value of the units attribute must not reference a units definition that contains <unit> elements that in turn directly or indirectly reference the current units definition.
[ This rule prevents circular units definitions. It must be possible to break down a complex units definition into the base SI units. ]
- Allowed values of the
prefix attribute
-
If present, the value of the prefix attribute must be an integer or a name taken from one of the name columns of Table 3.
[ The unit is scaled by 10 raised to the power of the specified integer or the factor corresponding to the specified name. Therefore, prefix attribute values of "centi" and "-2" are equivalent. ]
-
If not present, the value of the prefix attribute defaults to "0".
- Allowed values of the
exponent attribute
-
If present, the value of the exponent attribute must be a real number.
-
If not present, the value of the exponent attribute defaults to "1.0".
- Allowed values of the
multiplier attribute
-
If present, the value of the multiplier attribute must be a real number.
-
If not present, the value of the multiplier attribute defaults to "1.0".
- Allowed values of the
offset attribute
-
If present, the value of the offset attribute must be a real number.
-
If not present, the value of the offset attribute defaults to "0.0".
- Proper use of the
offset attribute
-
A <units> element containing a <unit> element that defines an offset attribute with a value other than "0.0" must not contain other <unit> elements.
[ The offset attribute can only be used in a simple units definition, as defined in Section 5.2.3. ]
-
A <unit> element that defines an offset attribute with a value other than "0.0" must not define an exponent attribute with a value other than "1.0".
[ The offset attribute can only be used in a simple units definition, as defined in Section 5.2.3. ]
The <units> element may be placed inside both <model> and <component> elements. When user-defined units are referenced by a variable or number declaration inside a component, the units definition is first looked for inside the current <component> element. If a matching units definition cannot be found, then the units definition is looked for in the parent <model> element.
Two units references are considered identical if they satisfy one of the following criteria:
- They reference the same units definition from the standard dictionary.
- They reference the same units definition in the current
<component> element. - They reference the same units definition in the current
<model> element, where that units definition is not superceded by a units definition with the same name in the current <component> element.
Two sets of units are considered equivalent if, when each is recursively resolved until left with nothing but products of SI and user-defined base units:
- the resolved form of each units definition consists of the same set of base units, and
- the exponent on each base unit is identical in each resolved units definition.
If software claims to perform dimension consistency checking of equations or conversion of units when mapping variables, it must obtain results that are equivalent to those produced using the algorithms described in Section 5.5.5 and Section 5.5.6, respectively. Both of these algorithms use the algorithm described in this section to expand units definitions into functions of the SI and user-defined base units.
This section derives a mathematical expression that relates units U to standard and user-defined base units. The specific steps in the derivation depend on whether the units definition for U is simple or complex, as defined in Section 5.2.3. Both derivations use recursive methods. At each step, any units that are not base units are replaced with expansions based on the appropriate definition.
The resolution of a simple units definition is straightforward, because the subunits on which the new units are based are also simple units. If units U are simple units, then the definition of U is given by:
xU[ U ] = ( m1 [ U/u1 ] p1 ) x1 [ u1 ] + o1 [ U ] (1)
where m1, o1, p1 and u1 are the values of the multiplier, offset, prefix, and units attributes on the <unit> element respectively, and u1 is another simple units definition given by:
x1[ u1 ] = ( m2 [ u1/u2 ] p2 ) x2 [ u2 ] + o2 [ u1 ] (2)
Equation 2 can be substituted into Equation 1 to give:
xU[ U ] = ( m1 [ U/u1 ] p1 ) ( ( m2 [ u1/u2 ] p2 ) x2 [ u2 ] + o2 [ u1 ] ) + o1 [ U ] (3)
Further levels of units definitions can be rearranged and resolved to simpler units as shown above until the resulting expression relates U to some base units. This final expression can be simplified to be in the following form.
xU[ U ] = mn [ U/un ] xn [ un ] + on [ U ] (4)
where un represents the final base units, and the constants mn and on are the result of the conversion of prefixes into scale factors according to the Table 3 and simplification.
For a complex units definition, the units U can be related to the subunits that are referenced in the definition using the following expression:
xU [ U ] = x1 [ u1e1 ... unen ] m1 [ U1/n / u1e1 ] p1e1 ... mn [ U1/n / unen ] pnen (5)
where mn, pn, un, and en refer to the values of the multiplier, prefix, units, and exponent attributes on the n-th <unit> element in the units definition respectively. Any units that appear in the expansion of the first units definition that are not base units should be expanded using the appropriate equation. The resulting expansion is then substituted directly into the parent expression in place of the relevant units reference. This expansion and substitution is performed recursively until the unit definitions referenced in the expression are base units.
It is very important to note that when a simple unit definitions is encountered in the expansion of a complex units definition, the fully expanded form of that simple units definition should be substituted into the parent expression without the constant offset term.
The final expansion can be simplified into the following form:
xU [ U ] = xn [ u1e1 ... unen ] mn [ U / u1e1 ... unen ] (6)
where mn is the multiplier resulting from the conversion of prefixes into scale factors according to the Table 3 and simplification, and un and en are the units name and corresponding exponent for the n-th base units.
Some examples of the expansion of units definitions will be made available soon.
If software chooses to verify that equations are self-consistent with respect to the dimensions of the units definitions referenced by all numbers and variables, it must obtain the same results as would be obtained by following these steps:
-
The equation is split into a tree of equation parts, in which each parent part is obtained by the application of a single operator to its children. A relational operator (typically the equals operator) combines the nodes at the top of the tree. An example of the tree formulation of an equation is given in Section 5.3.2. This specification will not attempt to further define this step.
-
The units definitions for the terms at the leaves of the tree are expanded into functions of the SI and user-defined base units. The expansion of a units definition into base units is discussed in Section 5.5.4.
-
Starting at the leaves of the tree, sets of child nodes can be recursively removed from the tree according to the operator applied to them. Operators such as addition or subtraction require that all of the child nodes have unit definitions with identical dimensions, as defined in Section 5.5.3. If this is true, the parent node assumes the same dimensions as its children. If it is not, the equation has inconsistent dimensions. There are no restrictions on the units definitions used by nodes combined using operators such as multiplication or division operators. The dimensions of the parent term assume the result of the appropriate operation on the dimensions of the child terms.
-
The equation has self-consistent dimensions if the fully expanded units definitions of the two nodes at the top of the tree are equivalent, as defined in Section 5.5.3.
-
It an inconsistency is detected at any point, then software is free to do whatever it likes. This specification recommends that it alert the user to a possible error, at the very least.
If software claims to be able to perform units conversion when passing the value of a variable between components, it is required to produce results that are consistent with those that would be obtained using the algorithm described in this section.
If two variable declarations both reference identical units definitions as defined in Section 5.5.2, then there is a one-to-one mapping between the the variable's value in both components.
If two variable declarations reference different units definitions, some sort of units analysis and conversion is required to ensure that the model functions properly. If software chooses to perform this variable mapping, then it must be capable of converting any value of a variable x which is measured in U1 units to an equivalent value y measured in U2 units. This conversion must obtain the same results as would be obtained by following the procedure outlined below to derive a mathematical expression relating x to y:
-
Two mathematical expressions are generated, in which
U1 and U2 are functions of SI and user-defined base units. The method by which these expressions are generated is discussed in Section 5.5.4.
-
U1 and U2 must have equivalent dimensions as defined in Section 5.5.3.
-
The expression relating
U1 to the base units is inverted, and combined with the expression for U2 to give a single expression relating x to y. This inversion and substitution process is discussed in Section 5.5.7.
The recursive resolution of units definitions according to the procedure defined in Section 5.5.4 leaves two equations that are of one of the following two forms:
znew[ U ] = m [ U/un ] zold [ un ] + o [ U ] (1)
znew [ U ] = zold [ u1e1 ... unen ] m [ U / u1e1 ... unen ] (2)
In most cases, both equations will be of the same form. If the expressions for U1 and U2 are of different forms, the two equations will only have equivalent dimensions if the expression of form shown in Equation 2 has a single base unit u1, and e1 has a value of one.
The expanded equations for U1 and U2 can be related by either un, if the expressions are of the form shown in Equation 1, or by the product u1e1 ... unen, if the equations are of the form shown in Equation 2. The equation for x can be inverted. This inversion will result in one of the forms shown below:
zold[ un ] = ( znew [ U ] - o [ U ] ) / m [ U/un ] (3)
zold [ u1e1 ... unen ] = znew [ U ] / mn [ U / u1e1 ... unen ] (4)
The inverted equation for x can be substituted into the equation for y to give a single equation defining y in terms of x. Examples of this procedure will be made available soon.
|