CellML Specification Draft — 2 March 2001

Get the PDF!

Status of this document

This document is a preliminary version of the specification for version 1.0 of CellML^TM. It is distributed for discussion purposes only, and should not be used as a reference. The definitive version of the CellML specification can always be found on the CellML website: http://www.cellml.org/public/specification/index.html

A message will be posted to the cellml-announce mailing list when a full candidate specification is available. You can join the cellml-announce mailing list at: http://www.cellml.org/mailman/listinfo.

Feedback on this document should be sent to the cellml-discussion mailing list. You can join this mailing list at: http://www.cellml.org/mailman/listinfo. Note that members of the cellml-discussion mailing list will receive all posts to cellml-announce, so it is not necessary to join both lists. If you wish to provide feedback, but do not want to join the cellml-discussion mailing list, you can e-mail your comments to mailto:info@cellml.org.

All sections of this specification are subject to change. The following items are currently under review, and will almost certainly change:

• The syntax for variable mapping
• The syntax for grouping, as well as some details of the data model for grouping
• The algorithm for the expansion of units definitions

In addition, we intend to add the following content to the specification before the full candidate specification is released:

• The conformance level of each rule (see the introduction section of the current document for more information about conformance levels)
• Additional examples in the units section
• Further specification of the mathematics and scripting functionality (the mathematics section of the current document indicates which portions are targeted for improvement)
• An initial draft of the companion CellML metadata specification

Contents

• 1  Introduction
• 2  Fundamentals
• 3  Model Structure
• 4  Mathematics
• 5  Units
• 6  Grouping
• 7  Reactions
• 8  Metadata Framework

1  Introduction

1.1  Introduction to CellML

This document formally specifies CellML^TM, an XML-based language for describing and exchanging a wide range of mathematical models of cells and subcellular processes. CellML is being developed by scientists in the Bioengineering Research Group at the University of Auckland and at Physiome Sciences, Inc. The development of CellML is guided by an advisory board drawn from many different areas of biological modelling (see the project team page on the CellML website for more information). CellML is being developed as an open standard, and all interested parties are encouraged to send feedback to info@cellml.org, or to the cellml-discussion mailing list.

1.1.1  Purpose and scope of CellML

CellML is intended to support the definition of any type of model of a cell or subcellular process. Therefore, it uses a very general structure. CellML is also intended to facilitate the re-use of models and parts of models. It accomplishes this by using a component-based architecture. Models are split into logical sub-parts called components. These components are then connected together to form a model.

The scope of CellML is specifically limited to the definition of model structure. All other types of information that modellers need or want to include in a model document are incorporated using other languages. For instance, mathematics is included in CellML documents using MathML. Metadata is included as RDF, using the Dublin Core's schema wherever possible.

1.1.2  What is XML?

The CellML language is defined in terms of a meta-language called XML, which stands for eXtensible Markup Language. XML is a standard published by the World Wide Web Consortium, the organisation responsible for defining many internet-related standards, most notably HTML. XML is essentially a means of adding structure to text documents, allowing machines to unambiguously associate text or binary data with a particular component in a document's data model.

XML is an appropriate medium for CellML because it is both human and machine readable. A model author can create a CellML document with a text editor or with any piece of CellML-compliant software. XML is a well-defined and widely used specification, and many free software utilities and libraries for the processing of XML already exist, simplifying the development of CellML software. XML has also been designed to be usable over the internet, making CellML suitable for the interchange of models between software and databases at different physical locations.

A quick introduction to XML is available in the examples section of the CellML website.

1.1.3  Definition of "model"

A model is an idealized representation of the rules that govern the behaviour of a system. CellML supports both quantitative and qualitative models. Quantitative models represent these rules using mathematics. Qualitative models represent the relationships between objects in the system, without attempting to define mathematics to represent the behaviour of the objects.

The CellML specification covers three kinds of models: complete, incomplete, and partial. A complete quantitative model is one that can be simulated (i.e., the mathematical equations contained in the model can be solved). A complete qualitative model is one in which all objects of interest in a system are represented. An incomplete model is a work in progress. For instance, an incomplete quantitative model might not contain all of the equations necessary to simulate the behaviour of the system. A partial model is a description of one aspect of the system. Within that portion of the system, the description is complete. However, it still might not be possible to run a simulation of the model.

A valid CellML document may describe a complete, incomplete, or partial model. A valid CellML model must be complete. This specification does not attempt to limit the behaviour of processing software when confronted with invalid documents or models. It is recommended that software report errors to the modeller (at the very least).

1.2  Structure of the CellML Specification

1.2.1  Sections of the CellML specification

The CellML specification is divided into several sections, each of which discusses a particular aspect of CellML:

• Fundamentals — This section explains concepts used in all other sections of the specification, such as the definition of a valid CellML name and the use of XML namespaces in CellML.
• Model Structure — This section describes how models are organised in CellML. It includes an explanation of the use of a network of components to define a model and a discussion of variables in CellML.
• Mathematics — This section describes how to define mathematical equations and algorithms in CellML models.
• Units — This section explains the requirements for units in CellML and details how a modeller can define arbitrary sets of units.
• Grouping — This section explains how a model can be organised into logical encapsulation and geometric containment hierarchies by grouping components.
• Reactions — This section introduces the CellML syntax that makes it possible to define the chemical expressions that make up reaction/pathway models without resorting to MathML.
• Metadata — This section describes how to define metadata and associate it with models, model components, and other CellML elements.

A valid CellML model can be created using nothing beyond the material covered in the fundamentals, basic model structure, mathematics, and units sections of the specification. The concepts in the remaining sections of the specification allow modellers to build more meaningful models.

Each section of the specification is further divided into five subsections:

• Introduction — This subsection explains the purpose of the elements covered in the current section.
• Basic Structure — This subsection describes the new elements and attributes introduced in the current section of the specification and how they are combined.
• Examples — This subsection provides one or two basic examples of the correct use of the elements and attributes introduced in the current section of the specification. More extensive examples can be found in the examples section of the CellML website.
• Rules for CellML Documents — This subsection provides formal rules for the use of the elements and attributes introduced in the current section to create valid CellML documents. These rules are specified as bulleted lists. Each rule may have an associated explanation, which appears directly after the rule, in square brackets ([]).
• Rules for Processor Behaviour — This subsection provides some rules for correct CellML processor behaviour with regards to the elements and attributes introduced in the current section.

1.2.2  Levels of CellML conformance

The rules in the CellML specification can be split into two groups: rules that define the syntax of a CellML document and rules that determine how software processing that document should behave. In the subsequent sections of the specification, the first set of rules are included in subsections titled Rules for CellML Documents, and the second set is in subsections titled Rules for Processor Behaviour.

The rules can also be split into two groups, each representing different levels of conformance to the specification. The majority of the rules in the CellML specification are part of the first level of conformance. Rules that are part of the second level of conformance are indicated as such by the inclusion of the phrase "Level Two" after the rule statement. The meaning of these conformance levels for documents and processing software is discussed below.

The levels of conformance to the CellML specification should not be confused with the features defined in different versions of the specification. As CellML is developed further, future versions of the CellML specification will add new elements to the language, which may add document and behaviour rules that affect both levels of conformance. Features that are expected to be added to CellML are documented in the Future Directions part of the CellML website.

CellML conformance level one

The first level of CellML conformance is composed of the majority of rules in the CellML specification. Level one document rules generally specify how the different XML elements and attributes that make up the CellML vocabulary may be combined. A typical level one rule for a document is "Both the <model> and <component> elements can contain any number of <units> elements". Level one processor rules generally specify implied behaviour that is not immediately obvious from analysis of the XML. A typical level one rule for processor behaviour defines the scope of a units definition (see Section 5.5.1).

A CellML Document is conformant to level one of the CellML specification if it complies with all level one rules for documents in the CellML specification.

A CellML processor is conformant to level one of the CellML specification if it can validate CellML documents against all level one rules for documents in the CellML specification and it follows all appropriate level one rules for processor behaviour in the CellML specification when interpreting CellML documents. The appropriate rules are those that relate to the intended use of the software (i.e., software that only renders the model need not address the scope of units definitions).

CellML conformance level two

The second level of CellML conformance rule is composed of all of the rules from level one plus additional rules that are marked as belonging to level two in the specification. Currently, there are no level two document rules. Level two processor rules generally specify complex interactions between objects defined in different parts of a CellML document. A typical example is the requirement that all mathematics within a model be self-consistent.

A CellML document is conformant to level two of the CellML specification if it complies with all level one and level two rules for documents in the CellML specification.

A CellML processor is conformant to level two of the CellML specification if it can validate CellML documents against all level one and level two rules for documents in the CellML specification and it follows all appropriate level one and level two rules for processor behaviour in the CellML specification when interpreting CellML documents. The appropriate rules are those that relate to the intended use of the software (i.e., software that only renders the model need not address the consistency of mathematics).

2  Fundamentals

2.1  Introduction

The fundamentals section of the CellML specification introduces some concepts that are used throughout the entire language, and defines rules that are referenced in all or many of the other parts of the specification. These include the definition of names in CellML and recommended practice for the use of namespaces in CellML.

2.2  Basic Structure

2.2.1  Definition of a valid CellML identifier

The most common use of a CellML identifier is the name attribute required on many basic elements in CellML. The value of this attribute can be used to reference that element from elsewhere in the model definition or from another model definition altogether. An object's name can generally be thought of as a unique identifier for that object. Although the XML specification defines a mechanism for specifying that the value of an attribute is unique across an entire document (with the ID attribute type), we choose not to make use of that functionality because an object's name need only be unique across its own class of objects.

The generation of computer code for running simulations is one of the target applications for CellML. The value of an object's name attribute is intended to be a suitable name for the same object when it is represented in computer code. For this reason, CellML identifiers must consist of only alphanumeric characters and the underscore character ("_") and are subject to some additional constraints outlined below. These names will generally not be the most effective way of identifying the object to humans working with CellML models, as it is not possible to include whitespace or formatting. More human readable names can be defined and associated with CellML objects using the metadata functionality introduced in Section 8.

The XML specification is based on the Unicode standard, which defines a scheme for 16 bit character encoding. Thus it is possible to include, for instance, Japanese characters in a valid XML document. In the interests of making the code generation process as convenient as possible for those using mainstream programming languages, CellML identifiers are subject to the following constraints:

• An identifier must consist only of alphanumeric characters from the US-ASCII character set and underscore characters,
• An identifier must start with a letter or underscore,
• If an identifier starts with an underscore, then the second character must be a letter.

Convenient code generation is also the reason why colons, periods, and hyphens may not appear in CellML identifier. CellML identifiers are case sensitive: a variable with an identifier of ABC is different from a variable with an identifier of abc.

The specification of a valid CellML identifier is identical to the definition of a valid object name in SBML. This should simplify the process of translating model definitions between the two languages.

2.2.2  Namespaces in CellML

Namespaces in XML is a companion specification to the main XML specification. It provides a facility for associating the elements and/or attributes in all or part of a document with a particular schema, as indicated by a Uniform Resource Identifier (URI). The key aspect of the URI is that it is unique. The value of the URI need not have anything to do with the XML document that uses it, although typically it would be a good location for the XML Schema or DTD that defines the rules for the document type. The URI may be mapped to a prefix, which may then be used in front of element and attribute names, separated by a colon. If not mapped to a prefix, the URI sets the default schema for the current element and all of its children.

The CellML specification defines a small number of elements and attributes and a namespace with which they must be associated. Associating CellML elements and attributes with the CellML namespace allows them to be differentiated from elements and attributes from other vocabularies with which CellML syntax might be combined in a CellML document. For instance, CellML makes use of the MathML vocabulary for the definition of equations, and all MathML elements must be placed in the MathML namespace in order for CellML processing software to recognise those elements. Applications that store their own proprietary data within a CellML document must define their own namespaces, and associate their own elements and attributes with those namespaces, as discussed in Section 2.2.3.

The scope of CellML is specifically limited to the definition of model structure. The CellML namespace includes all elements and attributes that define the structure of a model. All other information that may be included in a CellML document, such as mathematics and metadata, is included using other namespaces. Metadata is placed in a variety of namespaces, as described in Section 8. The MathML namespace is given special importance, because content in this namespace is considered as fundamental as content in the CellML namespace. An empty CellML element may not contain content in either the CellML or MathML namespace, although it may contain content in other namespaces, including the metadata namespaces defined in this specification.

Table 1 defines all of the namespaces used in the rules defined in this specification. The first three namespaces are in the cellml.org domain, and are associated with the core model structure elements, some custom metadata elements, and an XML serialization of the Object Management Group's bibliographic query service (BQS) data model created for storing citations in CellML. The MathML and RDF namespaces are defined in standards administered by the World Wide Web Consortium. Finally, the Dublin Core and Dublin Core Qualifiers namespaces reference standards for metadata specification administered by the Dublin Core organisation.

Table 1 The CellML specification defines the expected behaviour of CellML processing software for XML elements and attributes that are in these namespaces. Applications may not place their own elements and attributes in these namespaces. See text for more details.

Table 1 also gives the recommended prefix to be mapped to each namespace declaration for use in CellML documents. It is recommended that when a CellML element such as <model> is the root element of a document, CellML be declared as the default namespace for the document and also be explicitly mapped to the cellml prefix. This simplifies the association of elements and attributes with the CellML namespace in regions of the document where the default namespace is not the CellML namespace. For instance, the MathML elements used to define equations are typically placed inside a <math> element that changes the default namespace to the MathML namespace. A cellml:units attribute in the CellML namespace can then be added to each of MathML's <cn> elements without having to redeclare the CellML namespace every time it is used.

2.2.3  Extending CellML documents

CellML processing software may store information not covered by the CellML specification in a CellML document by defining its own elements and attributes and placing them in a namespace other than one of those defined in Table 1. (This specification only defines the content models of elements in the namespaces in Table 1 with respect to other elements in those namespaces.) Elements and attributes in extension namespaces may appear anywhere in a CellML document, as long as the result is well-formed XML. Because the CellML specification is only concerned with content in the CellML or MathML namespaces, elements in extension namespaces may even appear inside elements defined by the CellML specification to be empty.

It is hoped that CellML processing applications will respect the extension elements and attributes of other applications. If a model is created in application A, which adds its own extension elements, and is subsequently edited in application B, it would be polite if application B included application A's extension elements in its output, even if these extension elements are now invalid. Applications will need to validate their own extension data if a CellML document is read in from a non-trusted location.

The namespace extension mechanism provides a convenient way to associate a small amount of application-specific information with a model defined in CellML. However, it is recommended that applications needing to store large amounts of information, such as rendering or simulation information, do so in a separate document. This will make CellML documents easier to exchange, and will prevent the loss of application-specific information if the model is read into another application.

2.3  Examples

Figure 1 contains some example CellML elements, each of which defines a name attribute. The values of the name attribute on the first three elements are valid CellML identifiers. The values of the name attribute on the last two elements are invalid identifiers.

<!--
  The following elements have name attributes with valid values.
-->

<component name="my_favorite_component" />

<variable name="_ca2_conc" units="millimolar" />

<model name="model1345" />

<!--
  The following elements have name attributes with invalid values.
  Names may not start with numbers or contain colons.
-->

<component name="123component" />

<component name="my_model:my_component" />

Figure 1 XML elements defining name attributes. Valid and invalid CellML identifiers are shown, as noted in the comments.

Figure 2 contains portions of a typical CellML document that demonstrate the recommended use of namespaces. The root element sets the default namespace to the CellML namespace and also explicitly maps the CellML namespace to the cellml prefix. The <math> element that encloses a set of equations inside a component element resets the default namespace to the MathML namespace. The units attribute on the <cn> element (which is in the MathML namespace) is placed in the CellML namespace by using the previously-defined cellml prefix.

<model
    name="simple_electrophysiological_model"
    xmlns="http://www.cellml.org/2001/03/cellml"
    xmlns:cellml="http://www.cellml.org/2001/03/cellml">
  
  ...

  <component name="extra_cellular_space">
    ...
    <math xmlns="http://www.w3.org/1998/Math/MathML">
      <apply><eq />
        <apply><diff />
          <bvar><ci> time </ci></bvar>
          <ci> Na </ci>
        </apply>
        <apply><times />
          <cn cellml:units="dimensionless"> -1.0 </cn>
          <ci> I_Na </ci>
        </apply>
       </apply>
       ...
    </math>  
  </component>

  ...

</model>

Figure 2 A CellML fragment demonstrating the recommended use of namespaces in a CellML document. This fragment is taken from the simple electro-physiological model example on the CellML website.

Figure 3 demonstrates how software can embed its own information inside a valid CellML document using XML namespaces. The <model> element sets the default namespace to the CellML namespace, and maps the app prefix to an extension namespace (i.e., one not defined in Table 1). The app prefix is then used to define an <app:component_rendering_information> element and two attributes on a <component> element.

<model
    name="cellml_model_with_extensions"
    xmlns="http://www.cellml.org/2001/03/cellml"
    xmlns:app="http://www.software.com/cellml_processor">

  <app:component_rendering_information>
    cell : blue
    membrane : yellow
    channel : red
  </app:component_rendering_information>

  <component
      name="cell"
      app:component_type="cell"
      app:render_corners="100, 100, 400, 400" />

</model>

Figure 3 A CellML document demonstrating the use of XML namespaces to embed application specific data inside a CellML document. The extension namespace was invented for demonstration purposes only.

2.4  Rules for CellML Documents

2.4.1  Valid CellML identifiers

• The following is definition of a valid CellML identifier using Backus-Naur notation:
  

          letter ::= 'a'...'z','A'...'Z'
          digit  ::= '0'...'9'
          name   ::= {'_'} letter {letter | '_' | digit }
        

  [ A valid CellML name must start with a letter or underscore ("_"). If a name starts with an underscore, the next character must be a letter. A name may continue with any alphanumeric character or an underscore. Backus-Naur notation is described in Naur, P. (1960) "Revised Report on the Algorithmic Language ALGOL 60", Communications of the ACM, 3(5):299-314. ]

2.4.2  Extension namespaces

• Any element not in one of the namespaces defined in Table 1 is an extension element. Any attribute not in one of the namespaces defined in Table 1 is an extension attribute. Attributes without an explicit namespace declaration are assumed to be in the same namespace as their parent element. Although not explicitly stated, a document author may add elements and attributes in other namespaces anywhere in a CellML document without affecting its validity.

2.4.3  Proper use of the CellML namespace

• Only elements and attributes defined in the CellML specification may be placed in the CellML namespace. [ Documents containing unknown elements or attributes in the CellML namespace are invalid CellML documents. Rules regarding the use of elements in the other namespaces defined in Table 1 are given in the appropriate sections. ]

2.5  Rules for Processor Behaviour

2.5.1  Treatment of CellML identifiers

• CellML identifiers must be handled in a case-sensitive manner. [ Two CellML elements of the same type may be defined with identifiers of A and a. Processing software is expected to match the identifiers in a case-sensitive manner when those elements are referenced at other places in the document. ]

2.5.2  Treatment of extension namespaces

• CellML processing software is free to do whatever it wishes when it encounters elements and attributes that are not in one of the namespaces defined in Table 1. [ If the namespace is unrecognised, then software should probably alert the user to its presence. Polite software should attempt to store non-CellML data, so that it can write it out again when it exports the document. Software should validate its own non-CellML data carefully when reading documents from a non-trusted location. ]

3  Model Structure

3.1  Introduction

Any model can be described as a network of connections between self-contained components. A component is a functional unit that corresponds to a physical compartment, event, or species or that is just a convenient modelling abstraction. Components contain variables and mathematical relationships that manipulate those variables. Connections contain mappings between the variables of connected components.

3.2  Basic Structure

3.2.1  Definition of a model

A CellML model may be a complete, functional model; an incomplete model; or a partial model (as defined in Section 1.1.3). A model is declared with the <model> element. This is the usual root element for a CellML document. The <model> element for the simple electro-physiology example from the examples section of the CellML website is shown in Figure 4.

<model
    name="simple_electro_physiological_model"
    xmlns="http://www.cellml.org/2001/03/cellml"
    xmlns:cellml="http://www.cellml.org/2001/03/cellml">

  ...

</model>

Figure 4 The root element of an XML document containing a CellML model description is the <model> element shown above.

The <model> element has a name attribute that allows this model to be unambiguously referenced by other models. For instance, this would be necessary if the model were to be combined with other models or partial models to create a larger model. The namespace declarations on the <model> element shown in Figure 4 are discussed in Section 2.2.3.

A <model> element may contain any number of the elements in the following list in any order. The recommended practice is for elements placed within the <model> element to appear in the order given in the following list. This allows people to quickly find certain kinds of information within a CellML document.

• <units> — A modeller can declare a set of units to use in the model, as described in Section 5.
• <component> — Components are the smallest functional units in a model. Each component contains variables that represent the key properties of the component and mathematics that describe the behaviour of the portion of the system represented by that component.
• <group> — Groups allow the modeller to define logical and physical relationships between components. Groups are defined using the <group> element, as discussed in Section 6.
• <connection> — Connections are used to connect components to each other and to map variables in one component to variables in another. Connections are defined using the <connection> element, as discussed in Section 3.2.4.

The <model> element (and indeed any of the elements in a CellML document) may define metadata to provide context for that object. This metadata might include documentation, citations from literature, or a modification history for the current CellML object. Adding metadata to a CellML document is discussed in detail in Section 8.

3.2.2  Definition of components

Constructing a model from multiple components encourages the re-use of components. For instance, an electro-physiological model of a cell might be organised into components that represent various ion channels. All of the mathematics that describe the behaviour of the L-type calcium channel would be defined in a single component representing this particular ion channel. If a modeller wished to re-use the portion of the model representing the L-type calcium channel in another model, he or she would only need to copy this component.

A <component> element is used to declare a CellML component. It may only be used inside a <model> element or as the root element of a CellML document. A <component> element that is the root of a CellML document does not define a complete model. It would probably be part of a library of standard components that could be imported and used in models. Eventually, CellML will include a mechanism that simplifies such re-use of components. At the present time, the component would need to be physically copied into a model document to be used in that model.

A CellML <model> may contain any number of <component> elements. Each <component> must have a name attribute, the value of which is a unique identifier for the component within the current model. The value of the name attribute is used to reference the component in other parts of the model, such as in connections and groups.

A <component> may contain any of the elements in the following list in any order. Again, recommended practice is for elements placed within the <component> element to appear in the order given in the following list.

• <units> — A modeller can declare a set of units to use within the component, as described in Section 5.
• <variable> — A component may contain any number of <variable> elements, which define variables that may be mathematically related in the equation blocks contained in the component. Variables are discussed in Section 3.2.3.
• <reaction> — A component may contain <reaction> elements, which are used to provide chemical and biochemical context for the equations describing a reaction. It is recommended that only one <reaction> element appear in any <component> element. The definition of reaction information is described in Section 7.
• <math> — A component may contain a set of mathematical relationships between the variables declared in this component. These equations are marked up using MathML, as discussed in Section 4.

A <component> element is also a sensible place to define metadata, using the syntax presented in Section 8.

The definitions of two <component> elements are included in the example described in Section 3.3.

3.2.3  Definition of variables

Models are usually developed to simulate the behaviour of a number of variables that have physiological significance. Each variable in the model belongs to a single component, which may contain equations or scripts that modify the value of that variable. The value of a variable may be passed through connections into other components. The variable must also be declared in these components, which can then use the value of the variable in their own equations and scripts but may not modify it.

The <variable> element is used to declare a CellML variable. It can only be used inside a <component> element. Variables must define a name attribute, the value of which must be unique across all variables in the current component. The name of a variable is used when referencing variables inside connections (see Section 3.2.4) and reactions (see Section 7). All variables must also define a units attribute. The value of this attribute must correspond to one of the keywords in the CellML units dictionary or the value of the name attribute of a units element defined within the current component or model, as described in Section 5.

A <variable> element may also have the following attributes:

• initial_value — This attribute provides a convenient means for specifying the initial or default value of a scalar variable in a simulation with time as the independent variable. The variable's value may be reset or modified in equations or scripts in the current component. The initial values of variables need not be set in the model definition at all; they could instead be set in a configuration file loaded separately by the model processor.
• public_interface — This attribute specifies the interface exposed to components in the parent and sibling sets (see below). The public interface may have a value "in", "out", or "none". The absence of a public_interface attribute implies a value of "none".
• private_interface — This attribute specifies the interface exposed to components in the encapsulated set (see below). The private interface may have a value "in", "out", or "none". The absence of a private_interface attribute implies a value of "none".

When a variable is declared with either a public_interface or private_interface attribute value of "in", then the value of that variable can be imported from another component. Otherwise, a variable's value must be set and modified in the current component. The variable is then said to belong to or be owned by the current component.

Whether or not a component may obtain the value of a variable in another component depends on the public_interface and private_interface attributes on the variable declaration, and the place of the two components in the encapsulation hierarchy. Encapsulation allows the modeller to hide a complex network of components from the rest of the model and provide a single component as an interface to the hidden network. Encapsulation effectively divides the network into layers, where connections between the layers may only be made through the interface components.

The components to which any given component may connect can be divided into three distinct classes. The set of all components encapsulated by the current component is referred to as the encapsulated set. If the current component is encapsulated, then the encapsulating component is referred to as the parent, and the set of all other components encapsulated by the same parent is referred to as the sibling set. If the current component is not encapsulated, then it has no parent and the sibling set consists of all other components in the model that are not encapsulated. The encapsulation hierarchy and its effects on variable mapping are described in Section 6.

Eventually, it will be possible to specify the temporal and/or spatial variation of a variable's value using FieldML. The capability to include FieldML is still under development. At the present time, all variables must have singular values.

3.2.4  Definition of connections

Connections provide the mechanism for mapping variables declared within one component to variables in another component, allowing information to be exchanged between the various components in the network. There will be many such mappings present in a network. The mapping of variables involves the transfer of a variable's value from one component to another. This transfer may involve a conversion to account for the units in which each component expects the variable's value to be defined. (More information on units conversion can be found in Section 5.)

The complete set of variable mappings between any two components constitutes a connection. Only one connection may be created between any two components in a model. Each connection contains a pair of component references, indicating the two components involved in the connection. The two component references each contain an ordered list of variable references. Each variable contained in the first ordered list is mapped to the corresponding variable contained in the second ordered list. Mapping depends only on the order of the <variable_ref> elements in the two <component_ref> elements. It is not necessary for the variables that are to be mapped to each other to have the same name. However, the interface attributes of each pair of variables must be compatible — an "out" variable in one component's interface must map to an "in" variable in the other component's interface. The direction of each mapping is determined by the value of the public_interface attributes on the two variables: the value is always passed from the variable with an interface value of "out" to the variable with an interface value of "in". The value of a variable declared with an interface value of "out" may be passed out to any number of variables in other components declared with interface values of "in". The component to which a variable belongs is found by following the variable back from "in" to "out" interfaces defined by the model's connections.

The <connection> element is used to declare a CellML connection. It can only appear inside a <model> element.

Two <component_ref> elements are used to reference the components involved in the connection. Each <component_ref> element must define a component attribute, the value of which is the name of the component being referenced. Currently, this component must be defined within the current <model> element. It is anticipated that it will eventually be possible to reference components from other models, allowing models to be connected into larger models.

The <variable_ref> element is used to reference the variables being mapped between the two components in the connection. Each <component_ref> element may contain multiple <variable_ref> elements, but the number of <variable_ref> elements in each of the two <component_ref> elements within a <connection> must be equal. Each <variable_ref> element must define a variable attribute, the value of which is equal to the name attribute value of a variable declared in the component referenced by the parent <component_ref> element.

The CellML example discussed in Section 3.3 demonstrates the definition of a <connection> element.

3.3  Examples

Figure 5 contains a portion of the CellML encoding of the Hodgkin-Huxley squid axon model published in 1952. The excerpt contains the definitions of the components corresponding to the membrane and the sodium channel, and the connection between the two components. Most of the complexity from the full model definition has been left out for conciseness and clarity. This example is only used to demonstrate the standard use of the <component>, <variable>, and <connection> elements.

<model
    name="hodgkin_huxley_model_excerpt"
    xmlns="http://www.cellml.org/2001/03/cellml">
    
  <component name="membrane">
    <!-- the following variable is used in other components -->
    <variable
        name="V" initial_value="-75.0"
        public_interface="out" units="millivolt" />
    <!-- the following variables are imported from other components -->
    <variable name="time" public_interface="in" units="millisecond" />
    <variable name="i_Na" public_interface="in" units="microA_per_cm2" />
    <!-- the following variable is only used internally -->
    <variable name="C" initial_value="1.0" units="microF_per_cm2" />
    <math xmlns="http://www.w3.org/1998/Math/MathML">
      <apply><eq />
        <apply><diff />
          <bvar><ci> time </ci></bvar>
          <ci> V </ci>
        </apply>
        <apply><divide />
          <ci> i_Na </ci>
          <ci> C </ci>
        </apply>
      </apply>
    </math>
  </component>

  <component name="sodium_channel">
    <variable name="i_Na" public_interface="out" units="microA_per_cm2" />
    <variable name="time" public_interface="in" units="millisecond" />
    <variable name="V" public_interface="in" units="millivolt" />
    <math xmlns="http://www.w3.org/1998/Math/MathML">
      <apply cellml:name="i_Na_calculation"><eq />
        <ci> i_Na </ci>
        ...  <!-- a function of V & time -->
      </apply>
    </math>
  </component>

  <connection>
    <component_ref component="membrane">
      <variable_ref variable="V" />
      <variable_ref variable="i_Na" />
    </component_ref>
    <component_ref component="sodium_channel">
      <variable_ref variable="V" />
      <variable_ref variable="i_Na" />
    </component_ref>
  </connection>

</model>

Figure 5 A small portion of the CellML definition of the Hodgkin-Huxley squid axon model from 1952. This excerpt contains the definition of the components corresponding to the membrane and the sodium channel, and the connection between them. Much detail has been omitted, but this example clearly demonstrates the relationship between the <component>, <variable> and <connection> elements. See the text for more information.

The membrane component declares four variables, which are divided into four types. The first variable is called V, and it represents the membrane voltage in the model. It has a public_interface attribute value of "out", which indicates that the variable "belongs" to this component and that its value may be obtained by other components in the model via connections. It references a units definition by the name of millivolt (this definition is not included here), and is given an initial value of -75.0 millivolts.

The second and third variables are time and I_Na (sodium current). They are both declared with a public_interface attribute value of "in", which indicates that their value is obtained from another component via a connection. Finally, a variable C (capacitance) is declared. This <variable> element defines neither a public_interface or a private_interface attribute. Both of these attributes therefore assume the default value of "none", which means that the variable belongs to the current component and is not visible to other components in the model.

After the variable declarations, a <math> element in the MathML namespace is used to define an equation relating V to the other variables. Only the values of the variables belonging to a component may be mathematically modified in that component. The equation that appears in the full model is too lengthy to include here. Instead, a nonsense equation is included to demonstrate the use of mathematics in components. This equations is:

The sodium_channel component declares three variables, all of which represent quantities that were also declared in the membrane component. The I_Na variable declared in this component has a public_interface attribute value of "out", indicating that the sodium current belongs to this component. The value of the sodium current is calculated in this component, although the actual math has been omitted.

Finally, a <connection> element references the membrane and sodium_channel components (using <component_ref> elements) and maps the V and I_Na variables in each component together. Variables are mapped according to the order of <variable_ref> elements within each <component_ref> element.

3.4  Rules for CellML Documents

The following are the rules for using the <model>, <component>, <variable>, <connection>, and <component_ref> elements, and <variable_ref> elements within <component_ref> elements.

3.4.1  The <model> element

1. Allowed use of the <model> element
   • A <model> element must contain only the following elements, which may appear in any order:
     • <units>, <component>, <connection>, and <group> elements in the CellML namespace,
     • metadata framework elements, as described in Section 8.
     [ Recommended practice is to define the CellML namespace child elements in a <model> element in the order stated above. ]
   • Each <model> element must define a name attribute.
2. Allowed values of the name attribute
   • The value of the name attribute must be a valid CellML identifier as discussed in Section 2.2.1.

3.4.2  The <component> element

1. Allowed use of the <component> element
   • A <component> element must contain only the following elements, which may appear in any order:
     • <units> and <variable> elements in the CellML namespace,
     • <math> elements in the MathML namespace,
     • metadata framework elements, as described in Section 8.
     [ Recommended practice is to define the CellML and MathML namespace child elements of a <component> element in the order stated above. Note that it a <component> element must not appear inside another <component> element. Such nesting could be intended to indicate a logical encapsulation relationship, a geometric containment relationship, or some other relationship between the two components. There is no reason to assume that the nesting hierarchy produced for one type of relationship would be consistent with the hierarchy produced for other types of relationship. Therefore, CellML defines these relationships using the <group> element, rather than nesting of <component> elements. ]
   • Each <component> element must define a name attribute.
2. Allowed values of the name attribute
   • The value of the name attribute must be a valid CellML identifier as discussed in Section 2.2.1.
   • The value of the name attribute must be unique across all <component> elements contained in the same <model> element.

3.4.3  The <variable> element

1. Allowed use of the <variable> element
   • A <variable> element must contain only the following elements, which may appear in any order:
     • metadata framework elements, as described in Section 8.
   • Each <variable> element must define a name attribute and a units attribute. It may also define public_interface, private_interface, and initial_value attributes.
2. Allowed values of the name attribute
   • The value of the name attribute must be a valid CellML identifier as discussed in Section 2.2.1.
   • The value of the name attribute of a <variable> element must be unique across all <variable> elements contained in the same <component> element. [ Two variables in the same component may not have the same name. However, two variables in different components can have the same name, and a variable can have the same name as its parent component. ]
3. Allowed values of the units attribute
   • The value of the units attribute must either be one of the keywords defined in the standard dictionary or the value of the name attribute on a <units> element defined in the current component or model. [ The dictionary and the units element are described in Section 5. ]
4. Allowed values of the public_interface attribute
   • If present, the value of the public_interface attribute must be "in", "out", or "none".
   • If not present, its value defaults to "none".
5. Allowed values of the private_interface attribute
   • If present, the value of the private_interface attribute must be "in", "out", or "none".
   • If not present, its value defaults to "none".
6. Proper use of the public_interface and private_interface attributes
   • A <variable> element must not define both public_interface and private_interface attributes with values equal to "in". [ A variable's value may only be obtained via one mapping. ]
7. Allowed values of the initial_value attribute
   • If present, the value of the initial_value attribute must be a real number.
   • The absence of an initial_value attribute implies nothing. [ The absence of this attribute would usually mean either that the variable does not need an initial value or that this value will be supplied in a parameter file or by the user at the time simulations using the model are run. ]
8. Proper use of the initial_value attribute
   • An initial_value attribute must not be defined on a <variable> element with a public_interface or private_interface attribute with a value of "in". [ These variables receive their value from variables belonging to another component. ]

3.4.4  The <connection> element

1. Allowed use of the <connection> element
   • A <connection> element must contain only the following elements, which may appear in any order:
     • <component_ref> elements in the CellML namespace,
     • metadata framework elements, as described in Section 8.
   • Each connection element must contain exactly two <component_ref> elements.

3.4.5  The <component_ref> element in a <connection> element

1. Allowed use of the <component_ref> element in a <connection> element
   • A <component_ref> element in a <connection> element must contain only the following elements, which may appear in any order:
     • <variable_ref> elements in the CellML namespace,
     • metadata framework elements, as described in Section 8.
   • Each <component_ref> element in a <connection> element must contain at least one <variable_ref> element.
   • The two <component_ref> elements in a <connection> element must contain an equal number of <variable_ref> elements.
   • Each <component_ref> element must define a component attribute.
2. Allowed values of the component attribute
   • The value of the component attribute must equal the value of the name attribute of a <component> element contained within the current <model> element.
   • Every <connection> element in a model must contain a unique pair of component attributes on the child <component_ref> elements. [ There can only be one connection between any two components in a network. This prevents setting up inconsistent, circular, or duplicate variable mappings between any two components in the network. However, it does not prevent a model author from creating inconsistent mathematical relationships between the variables. ]

3.4.6  The <variable_ref> element in a <component_ref> element

1. Allowed use of the <variable_ref> element in a <component_ref> element
   • A <variable_ref> in a <component_ref> element must contain only the following elements, which may appear in any order:
     • metadata framework elements, as described in Section 8.
   • Each <variable_ref> element must define a variable attribute.
2. Allowed values of the variable attribute
   • The value of the variable attribute on a <variable_ref> element in a <component_ref> element must equal the value of the name attribute of a <variable> element contained in the <component> element referenced by the parent <component_ref> element.
3. Proper use of the <variable_ref> element to map variables to each other

   [ The rules for mapping a variable to other variables depend on the encapsulation hierarchy of the component that owns the variable. This hierarchy divides the rest of the components in the model into parent, sibling, and encapsulated sets, as described in Section 3.2.3. The public_interface attribute defines the availability of a variable to the parent component and components in the sibling set. The private_interface attribute defines the availability of a variable to components in the encapsulated set. ]

   • Variables with a public_interface or private_interface attribute value of "in" must be mapped to variables with a public_interface or private_interface attribute value of "out".
   • A variable with either a private_interface or public_interface attribute value of "in" may be mapped to no more than one other variable in the model. [ Note that a similar restriction does not apply to variables with interface values of "out". An output variable can be mapped to multiple input variables in various components in the current model. It is up to the modeller to ensure that these mappings are consistent. ]
   • A variable with a public_interface attribute value of "in" may be mapped to a single variable owned by a component in the sibling set, provided the target variable has a public_interface attribute value of "out", or to a single variable owned by the parent component, provided the target variable has a private_interface attribute value of "out".
   • A variable with a public_interface attribute value of "out" may be mapped to variables owned by components in the sibling set, provided the target variables have public_interface attribute values of "in". It may also be mapped to variables owned by the parent component, provided the target variables have private_interface attribute values of "in".
   • A variable with a private_interface attribute value of "in" may be mapped to a single variable owned by a component in the encapsulated set, provided the target variable has a public_interface attribute value of "out".
   • A variable with a private_interface attribute value of "out" may be mapped to variables owned by components in the encapsulated set, provided the target variables have public_interface attribute values of "in".

3.5  Rules for Processor Behaviour

3.5.1  Mapping of variables

• The lists of <variable_ref> elements are ordered. The first <variable_ref> element in the first <component_ref> element maps to the first <variable_ref> element in the second <component_ref> element, and so on. Variable mappings specifically do not depend on variable names.

4  Mathematics

4.1  Introduction

Model components may contain mathematical expressions that manipulate the values of variables that belong to the current component. These expressions are also free to use (but not change) the values of any other variables declared in the current component. Mathematical expressions must be defined using Mathematical Markup Language (MathML), an XML-based language that encodes the underlying structure of an expression. If it is not possible to describe a particular mathematical expression in MathML or if a model specifically prescribes a certain algorithm, model authors may make use of ECMAScript (formerly Netscape's Javascript) to encode algorithms.

The first version of MathML reached recommendation status at the World Wide Web Consortium (W3C) in April 1998. A second version was released in February 2001. CellML uses the content markup element set from MathML 2.0, which extends the functionality of MathML 1.0 in many key areas. The MathML 2.0 recommendation also deprecates the use of some MathML 1.0 elements. However, CellML processing software is expected to maintain compatibility with equations defined using MathML 1.0.

ECMA is an international industry association that develops standards in information and communication for the European union. ECMA took the scripting language that Netscape developed for adding interactive content to its web browser and developed the formal language specification ECMA-262 (ECMAScript Language Specification).

4.2  Basic Structure

4.2.1  Allowed locations of mathematical expressions

All mathematical expressions defined using MathML must be placed inside a <math> element in the MathML namespace. A math element must be a child of a <component> element or a <role> element (the <role> element is a child of the <variable_ref> element in a <reaction> element).

The CellML syntax for defining scripts using ECMAScript has yet to be determined. It is anticipated that this will involve a <script> element in the CellML namespace that may be placed in <model>, <component> or <role> elements.

Mathematical expressions and scripts may manipulate the variables belonging to the component in which they are defined and may use (but not change) the value of variables belonging to other components if necessary. The declaration of variables in CellML is specified in Section 3.

4.2.2  Allowed mathematical expressions

At the present time, all models defined in CellML consist solely of algebraic equations and ordinary differential equations. However, MathML can specify a wide-range of mathematics, not all of which will necessarily be interpretable by every CellML processor. To encourage interoperability of models created using different processors, the CellML development team intends to define groups of mathematical functionality. CellML processing software could then publish which groups of mathematical functionality it supports.

4.2.3  Definition of scripts

Scripts will be defined using ECMAScript. The CellML development team is still determining how best to incorporate these scripts into CellML.

The use of scripts in CellML is strongly discouraged. CellML is aimed at specifying a model in terms of its most basic governing equations. Wherever possible, mathematical equations should be used to specify the changing behaviour of a model's state variables.

When scripts are used, they are assumed to execute instantly with respect to any independent variables, making it possible for the integrator to ignore their execution.

4.3  Examples

The CellML fragment in Figure 6 demonstrates how MathML can be employed within CellML to define mathematical expressions. This fragment is part of the definition of a component that represents the behaviour of the n gate from the potassium channel in the Hodgkin-Huxley squid axon model of 1952. The component contains two units definitions, two variable declarations, and a block of MathML that defines the calculation of the alpha variable of the n gate. This equation has the form:

                         0.01(V + 10.0)
         alpha_n = --------------------------
                    exp(0.1(V + 10.0)) - 1.0

<component
    name="potassium_channel_n_gate"
    xmlns="http://www.cellml.org/2001/03/cellml">

  <units name="per_millisecond">
    <unit prefix="milli" units="second" exponent="-1" />
  </units>

  <units name="millivolt">
    <unit prefix="milli" units="volt" />
  </units>

  <variable name="alpha_n" units="per_millisecond" />
  <variable name="V" public_interface="in" units="millivolt" />

  <math xmlns="http://www.w3.org/1998/Math/MathML">
    <!--
      The alpha rate constant on the n gate is a function of membrane voltage.
    -->
    <apply cmeta:id="alpha_n_calculation"><eq />
      <ci> alpha_n </ci>
      <apply><divide />
        <apply><times />
          <cn cellml:units="per_millisecond"> 0.01 </cn>
          <apply><plus />
            <ci> V </ci>
            <cn cellml:units="millivolt"> 10.0 </cn>
          </apply>
        </apply>
        <apply><minus />
          <apply><exp />
            <apply><times />
              <cn cellml:units="dimensionless"> 0.1 </cn>
              <apply><plus />
                <ci> V </ci>
                <cn cellml:units="millivolt"> 10.0 </cn>
              </apply>
            </apply>
          </apply>
          <cn cellml:units="dimensionless"> 1.0 </cn>
        </apply>
      </apply>
    </apply>
  </math>

</component>

Figure 6 Part of the definition of a component that represents the behaviour of the n gate from the potassium channel in the Hodgkin-Huxley squid axon model of 1952. The component contains two units definitions, two variable declarations, and a block of MathML that defines the calculation of the alpha variable of the n gate. The <mathml:apply> element at the top level of the expression defines a cmeta:id attribute, which can be used to associate metadata (such as documentation) with the expression, as described in Section 8.

All of the <mathml:cn> elements in the equation define the required cellml:units attribute, which associates a units definition with the number delimited by the <cn> element. The inclusion of units in the equation allows CellML processing software to check that the dimensions on all terms in an equation are consistent, as defined in Section 5

The <mathml:apply> element at the top level of the expression defines a cmeta:id attribute, which can be used to associate metadata (such as documentation) with the expression as described in Section 8.

4.4  Rules for CellML Documents

4.4.1  The <mathml:math> element

1. Allowed use of the <mathml:math> element
   • The <mathml:math> element must only appear as a child of <cellml:component> or <cellml:role> elements. [ In this and subsequent rules, the use of the mathml and cellml prefixes indicates that elements and attributes are in the MathML and CellML namespaces, respectively. ]
   • The contents of a <mathml:math> element must conform to the Mathematical Markup Language (MathML) Version 2.0 recommendation from the W3C.

4.4.2  The <mathml:cn> element

1. Allowed use of the <mathml:cn> element
   • A <mathml:cn> element must define a cellml:units attribute. [ All bare numbers in MathML content markup are enclosed in a <cn> element in the MathML namespace.  ]
2. Allowed values of the cellml:units attribute
   • The value of the cellml:units attribute must be taken from the standard dictionary of units given in Section 5.2.1, or be the value of the name attribute on a <units> element defined in the current <component> or <model> element.

4.5  Rules for Processor Behaviour

4.5.1  Order of calculations

Any component may contain multiple blocks of equations and multiple scripts. The order of execution of equations in any block is not necessarily the order in which they appear. All non-differential equations will be calculated before differential equations. This allows the evaluation of parameters before they are input into differential equations. Processing software must determine the appropriate ordering for the calculation of equations across multiple blocks of equations and across the model in general.

Scripts are assumed to execute instantly with respect to the independent variable time, making it possible for the integrator to ignore their execution.

5  Units

5.1  Introduction

One of the key features ensuring robustness and re-usability of CellML components and models is the requirement that units be associated with all variables and numbers in a CellML document. This allows components and models that declare variables with different units to be connected, as long as variables that are mapped to one another have the same dimensions. For instance, it is possible to map a variable declared with units of "pound/foot" to a variable declared with units of "kilogram/metre", but not to a variable declared with units of "mole/litre" or "kilogram-squared/metre". The explicit declaration of units also allows CellML processing software to check the consistency of each equation in a model.

5.2  Basic Structure

5.2.1  Dictionary of standard units

CellML provides a dictionary of standard units that may be used in variable declarations or attached to bare numbers in mathematics. References to these units should make use of the actual name of the units, rather than the standard abbreviation, thus avoiding confusion between units (e.g., metre) and prefixes (e.g., milli). The full list of units that any CellML processing application is expected to recognise is given in Table 2. The keywords in the table comprise the SI base and derived units and some additional units commonly used in the types of biological models likely to be defined using CellML. Expressions relating these additional units to the SI base units are provided in Section 5.2.2. The only unfamiliar name on this list is dimensionless, which is used to indicate that a number or variable has no units associated with it.

Table 2 The dictionary of units keywords that CellML processing applications are expected to recognise. Base SI units are printed in bold text, derived SI units are printed in plain text, and additions to the standard units defined purely for the convenience of model authors are italicised.

This list is based on the ISO standard, including the year 2000 supplement. The American spellings of "meter" and "liter" are taken from the NIST Guide for the Use of the International System of UNITS (SI). The ISO standard defines the mathematical relationships between the derived SI units and the base SI units.

5.2.2  Definition of non-SI units

The CellML <units> elements in Figure 7 define the non-SI units in Table 2 (the italicised keywords) in terms of SI units. The format of the units element is formally specified in Section 5.2.3.

<!--
  x_new [celsius] = 1.0 [celsius/kelvin] x_old [kelvin] - 273.15 [celsius] 
-->
<units name="celsius">
  <unit offset="-273.15" units="kelvin" />
</units> 

<!--
  "dimensionless" is used for numbers that do not have units.
-->
<units name="dimensionless" />

<!--
  x_new [gram] = 0.001 [gram/kilogram] x_old [kilogram]
-->
<units name="gram">
  <unit multiplier="0.001" units="kilogram" />
</units>

<!--
  x_new [litre] = 1000 [litre/metre^3] (centi)^3 x_old [metre^3]
-->
<units name="litre">
  <unit multiplier="1000" prefix="centi" units="metre" exponent="3" />
</units>

Figure 7 These <units> elements define the non-SI units included in the standard CellML units dictionary in terms of SI units. The definition of liter is exactly the same as the definition of litre, and is therefore omitted. Note that these definitions must not be used in CellML documents: model authors are forbidden from defining units with the same names as those in the standard dictionary in Table 2.

5.2.3  User defined units

CellML also provides a facility whereby new units can be defined in terms of the units provided in the dictionary. This functionality allows the definition of units which are expressed as a scaled version of other units (as is the case for most imperial units), the definition of units which are made up of the product of other units, and even the creation of units that require an offset, such as degrees Fahrenheit. This allows model authors to work in whatever set of units they feel most comfortable, while still ensuring that their models can be integrated with those of other authors using other units.

New units are defined using the <units> element, which may be placed inside both <model> and <component> elements. When a <units> element is placed inside the <model> element, the units definition may be referenced from within any component in the model. When a <units> element is placed inside a <component> element, the units definition may only be referenced from within that component.

Each units element must define a name attribute, which is used to reference the units definition elsewhere. The value of the name attribute must be unique across all <units> elements in the <model> or <component> element in which it is defined. If the value of the name attribute of a <units> element defined inside a <component> element matches the value of the name attribute on a <units> element defined inside the parent <model> element, then it will redefine the units, and all references to these units within the component element refer to the new definition. Model authors must not redefine any of the standard units. Therefore, the value of the name attribute must not equal one of the names from the standard units dictionary in Table 2.

A <units> element may also define a base_units attribute, the associated behaviour of which is discussed in Section 5.2.4. A <units> element can contain a set of <unit> elements that reference units from the dictionary or some previously defined units.

A <unit> element has no content but may have up to five attributes. The units attribute is the only one that is required. It is used to set the base quantity for the current <unit> element, and its value must correspond to a keyword from the standard CellML units dictionary or to the value of the name attribute of a <units> element in the current component or model.

The definition of new units in terms of subunits may require the use of some combination of the optional offset, prefix, exponent, and multiplier attributes.

A multiplier attribute can be used to pre-multiply the quantity to be converted by any real scale factor. For instance, a multiplier of 0.45359237 is used to define a pound in terms of a kilogram. The multiplier attribute has a default value of "1.0"

The offset attribute is used to represent the addition of a constant in the transformation between the current units and the base units. This should only be necessary for the definition of temperature scales. For instance, an offset attribute value of "32.0" is needed to define Fahrenheit in terms of Celsius. The offset attribute has a default value of "0.0".

The prefix attribute can be used to indicate a scale for the referenced units. It is included primarily for the convenience of modellers who want to define units that differ from another units definition only by an SI scale factor. Its value must be from the standard set of CellML prefix names given in Table 3 or be an integer, in which case the units are pre-multiplied by 10 to the power of this number. The default value of the prefix attribute is "0.0", (the referenced units are scaled by a factor of one).

Table 3 The set of names that may be used in the prefix attribute on a <unit> element and the corresponding scale factors that will pre-multiply the unit. The standard abbreviation for each unit is provided for reference, but must not be used in the prefix attribute.

The scale factor described by the prefix attribute and the units referenced by the units attribute are raised to a power equal to the value of the exponent attribute. The value of the exponent attribute must be a floating point number, and is typically an integer. The exponent attribute has a default value of "1.0". Note that an exponent attribute value of "0.0" has the effect of removing the parent <unit> element from the current units definition.

A `simple units' definition occurs when units are defined as a linear function of some previously defined simple units or base units. This occurs when a <units> element contains only a single child <unit> element, that <unit> element has an exponent attribute value of "1.0", and the units definition referenced by the units attribute is one of the SI or user-defined base units or is itself a simple units definition. These are the only conditions under which a <unit> element may define an offset attribute. The formula that expresses how the old units (referenced by the value of the units attribute on the <unit> element) are transformed into the new units (defined by the value of the name attribute on the parent <units> element) is given below:

Terms in square brackets represent the units associated with a term in the expression, xold is the value to be transformed from the old units, xnew is the resulting value in the new units, Units are the units being defined, and multiplier, prefix, units, and offset correspond to the values of the appropriate attributes on the <unit> element.

`Complex units' are the product of multiple base quantities, and are created by placing several <unit> elements inside a single <units> element, or by defining an exponent attribute with a value other than "1.0" on any <unit> element. The conversion between the new units and the product of the constituent units is given by the formula below:

The mn, pn, un, and en terms refer to the values of the multiplier, prefix, units, and exponent attributes on the n-th <unit> element respectively. Note that this specification forbids offset attributes from being defined on any unit elements that occur inside a complex units definition.

It is very important to note that when a complex units definition references a simple units definition, any offset associated with the simple units definition is removed. This means that the conversions such as the one between degrees Fahrenheit per inch and degrees Celsius per centimetre involve only a scale factor.

5.2.4  New base units

A modeller might want to define and use units for which no simple conversion to SI units exist. A good example of this is pH, which is dimensionless, but uses a log scale. Ideally, pH should not simply be defined as dimensionless because software might then attempt to map variables defined with units of pH to any other dimensionless variables.

CellML addresses this by allowing the model author to indicate that a units definition is a new type of base unit, the definition of which can not be resolved into simpler subunits. This is done by defining a base_units attribute value of "yes" on the <units> element. This element must then be left empty. The base_units attribute is optional and has a default value of "no". If the base_units attribute is omitted or assigned a value of "no", units are expected to be defined in terms of other units as described in Section 5.2.3.

The indiscriminate use of the base_units attribute is strongly discouraged, because it has a significant impact on the re-usability of models and components. In particular, the base_units attribute should not be used to restrict users to creating models with an application-specific dictionary of units, as this prevents the efficient exchange of CellML models with other applications.

Software that is checking the consistency of the units in an equation (described in more detail in Section 5.2.5) can stop the recursive resolution of units definitions when the only remaining units are base SI units and user-defined base units.

5.2.5  Equation dimension checking

The association of units with every variable and bare number that appears in an equation in a CellML document provides CellML processing software the opportunity to perform equation dimension checking. Verifying that equations have consistent dimensions can potentially catch many basic mathematical errors. CellML Level One conformant software is free to ignore units in mathematics and assume that equations are consistent. CellML Level Two conformant software must check the consistency of dimensions in equations.

Section 5.5.5 specifies a possible implementation of equation dimensionality checking. This implementation splits an equation into a tree of equation parts, in which each parent part if obtained by the application of a single operator to its children. The units definition on each leaf node (i.e., part without children) is expanded into base units, as described in Section 5.5.4. The units definition for a node at a higher level of the tree is constructed by combining the units definition of its children. An equation has consistent dimensions if the fully expanded units definitions of the two nodes at the top level of the tree are equivalent, as defined in Section 5.5.3.

This specification does not require software to use the implementation discussed in Section 5.5.5, but does require that software that claims to perform dimension checking achieve the same results as if that implementation were used.

This specification does not attempt to completely prevent model authors from creating bad mathematics. Dimension consistency checking prevents modellers from adding variables with different dimensions but would not find errors in the following equations, which have different units but the same dimensions:

Although it would be technically possible to find and correct such errors, CellML processing software is not required to be able to do so.

5.2.6  Units and variable mapping

Associating units definitions with every variable declaration in a component allows variables from components that make use of different sets of units to be mapped together, as long as the variables have the same dimensions. Section 5.5.6 specifies a possible implementation of the conversion of a numeric value from one set of units to another. This specification does not require that software use this implementation but does require that software that claims to support units conversion during variable mapping achieve the same results as if this implementation were used.

This implementation generates an expression that relates each units definition to SI and user-defined base units. This expression is obtained by recursively expanding each units definition as described in Section 5.5.4, and then simplifying the result. The expression for the input units is then inverted to give an expression that relates the appropriate base units to the input units. This inverted expression is substituted into the expression for the target units, producing a single expression that relates the quantity to be converted from the input units to a corresponding quantity in the target units. The inversion and substitution process is described in Section 5.5.7.

5.3  Examples

5.3.1  Examples of user-defined units

Figure 8 shows several CellML units definitions, demonstrating how simple units can be expressed as linear functions of other simple units, and how complex units are obtained from the product of other units.

<!--
  Simple Units Definition 1
  x_new [fahrenheit] = 1.8 [fahrenheit/celsius] x_old [celsius] + 32.0 [fahrenheit]
-->
<units name="fahrenheit">
  <unit multiplier="1.8" offset="32.0" units="celsius" />
</units>

<!--
  Simple Units Definition 2
  x_new [rankine] = 1.8 [rankine/kelvin] x_old [kelvin]
-->
<units name="rankine">
  <unit multiplier="1.8" units="kelvin" />
</units>

<!--
  Simple Units Definition 2
  x_new [inch] = 2.54 [inch/metre] centi x_old [metre]
-->
<units name="inch">
  <unit multiplier="2.54" prefix="centi" units="metre" />
</units>

<!--
  Complex Units Definition 1
  x_new [millimolar] = milli x_old [ mole ( litre )^-1 ]
-->
<units name="millimolar">
  <unit prefix="milli" units="mole" />
  <unit units="litre" exponent="-1" />
</units>

<!--
  Complex Units Definition 2
  x_new [fahrenheit_per_inch] = x_old [ fahrenheit (inch)^-1 ]
-->
<units name="fahrenheit_per_inch">
  <unit units="fahrenheit" />
  <unit units="inch" exponent="-1" />
</units>

<!--
  Complex Units Definition 3
  x_new [celsius_per_centimetre] = x_old [ celsius (metre)^-1 ] (centi)^-1
-->
<units name="celsius_per_centimetre">
  <unit units="celsius" />
  <unit prefix="centi" units="metre" exponent="-1" />
</units>

Figure 8 Some examples of the use of the <units> element demonstrating the definition of simple and complex units.

5.3.2  Examples of equation tree formation

The first step in the algorithm proposed in Section 5.5.5 for verifying that a given equation has consistent dimensions is to convert the equation into a tree of equation parts. A relational operator (typically the equals operator) combines the nodes at the top of the tree. For instance, the equation:

would have the tree shown in Figure 9.

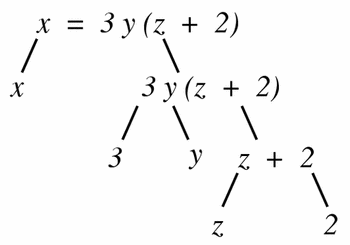
Figure 9 The tree form of the equation x = 3y(z + 2), in which each non-leaf node is obtained by the application of a single operator to its children.

5.4  Rules for CellML Documents

Units are a fundamental part of a CellML model definition. In this section, formal rules are specified for the system of units definition introduced in Section 5.2.

5.4.1  The <units> element

1. Allowed use of the <units> element
   • Both the <model> and <component> elements can contain any number of <units> elements.
   • Each <units> element must define a name attribute, and may define a base_units attribute.
   • If a <units> element defines a base_units attribute with a value of "yes", then that <units> element must contain only the following elements, which may appear in any order:
     • metadata framework elements, as described in Section 8.
   • If a <units> element does not define a base_units attribute with a value of "yes", then that <units> element must contain only the following elements, which may appear in any order:.
     • <unit> elements in the CellML namespace,
     • metadata framework elements, as described in Section 8.
2. Allowed values of the name attribute
   • The value of the name attribute must be a valid CellML identifier as discussed in Section 2.2.1.
   • The value of the name attribute must not equal one of the names defined in the standard dictionary of units in Table 2. [ Model authors may not redefine the standard units. ]
   • The value of the name attribute must be unique across all <units> elements at the same level in a CellML document. [ Two <units> elements in the same <model> element may not have the same name attribute value, although a <units> element in a <component> element may share the same name as a <units> element in the parent <model> element. In this case, the units definition in the <component> element supercedes the model-wide definition when referenced inside that component. ]
3. Allowed values of the base_units attribute
   • If present, the value of the base_units attribute must be "yes" or "no".
   • If not present, the value of the base_units attribute defaults to "no".

5.4.2  The <unit> element

1. Allowed use of the <unit> element
   • A <unit> element must contain only the following elements, which may appear in any order:
     • metadata framework elements, as described in Section 8.
   • Each <unit> element must define a units attribute. It may also define prefix, exponent, multiplier, and offset attributes.
2. Allowed values of the units attribute
   • The value of the units attribute must be taken from the standard dictionary of units listed in Table 2 or be the value of the name attribute on a <units> element defined in the current <component> or <model> element.
   • The value of the units attribute must not reference a units definition that contains <unit> elements that in turn directly or indirectly reference the current units definition. [ This rule prevents circular units definitions. It must be possible to break down a complex units definition into the base SI units. ]
3. Allowed values of the prefix attribute
   • If present, the value of the prefix attribute must be an integer or a name taken from one of the name columns of Table 3. [ The unit is scaled by 10 raised to the power of the specified integer or the factor corresponding to the specified name. Therefore, prefix attribute values of "centi" and "-2" are equivalent. ]
   • If not present, the value of the prefix attribute defaults to "0".
4. Allowed values of the exponent attribute
   • If present, the value of the exponent attribute must be a real number.
   • If not present, the value of the exponent attribute defaults to "1.0".
5. Allowed values of the multiplier attribute
   • If present, the value of the multiplier attribute must be a real number.
   • If not present, the value of the multiplier attribute defaults to "1.0".
6. Allowed values of the offset attribute
   • If present, the value of the offset attribute must be a real number.
   • If not present, the value of the offset attribute defaults to "0.0".
7. Proper use of the offset attribute
   • A <units> element containing a <unit> element that defines an offset attribute with a value other than "0.0" must not contain other <unit> elements. [ The offset attribute can only be used in a simple units definition, as defined in Section 5.2.3. ]
   • A <unit> element that defines an offset attribute with a value other than "0.0" must not define an exponent attribute with a value other than "1.0". [ The offset attribute can only be used in a simple units definition, as defined in Section 5.2.3. ]

5.5  Rules for Processor Behaviour

5.5.1  Resolving references to units definitions

The <units> element may be placed inside both <model> and <component> elements. When user-defined units are referenced by a variable or number declaration inside a component, the units definition is first looked for inside the current <component> element. If a matching units definition cannot be found, then the units definition is looked for in the parent <model> element.

5.5.2  Equivalence of units definitions

Two units references are considered identical if they satisfy one of the following criteria:

• They reference the same units definition from the standard dictionary.
• They reference the same units definition in the current <component> element.
• They reference the same units definition in the current <model> element, where that units definition is not superceded by a units definition with the same name in the current <component> element.

5.5.3  Dimensional equivalence of units definitions

Two sets of units are considered equivalent if, when each is recursively resolved until left with nothing but products of SI and user-defined base units:

• the resolved form of each units definition consists of the same set of base units, and
• the exponent on each base unit is identical in each resolved units definition.

5.5.4  Expansion of units definitions

If software claims to perform dimension consistency checking of equations or conversion of units when mapping variables, it must obtain results that are equivalent to those produced using the algorithms described in Section 5.5.5 and Section 5.5.6, respectively. Both of these algorithms use the algorithm described in this section to expand units definitions into functions of the SI and user-defined base units.

This section derives a mathematical expression that relates units U to standard and user-defined base units. The specific steps in the derivation depend on whether the units definition for U is simple or complex, as defined in Section 5.2.3. Both derivations use recursive methods. At each step, any units that are not base units are replaced with expansions based on the appropriate definition.

The resolution of a simple units definition is straightforward, because the subunits on which the new units are based are also simple units. If units U are simple units, then the definition of U is given by:

where m1, o1, p1 and u1 are the values of the multiplier, offset, prefix, and units attributes on the <unit> element respectively, and u1 is another simple units definition given by:

Equation 2 can be substituted into Equation 1 to give:

Further levels of units definitions can be rearranged and resolved to simpler units as shown above until the resulting expression relates U to some base units. This final expression can be simplified to be in the following form.

where un represents the final base units, and the constants mn and on are the result of the conversion of prefixes into scale factors according to the Table 3 and simplification.

For a complex units definition, the units U can be related to the subunits that are referenced in the definition using the following expression:

where mn, pn, un, and en refer to the values of the multiplier, prefix, units, and exponent attributes on the n-th <unit> element in the units definition respectively. Any units that appear in the expansion of the first units definition that are not base units should be expanded using the appropriate equation. The resulting expansion is then substituted directly into the parent expression in place of the relevant units reference. This expansion and substitution is performed recursively until the unit definitions referenced in the expression are base units.

It is very important to note that when a simple unit definitions is encountered in the expansion of a complex units definition, the fully expanded form of that simple units definition should be substituted into the parent expression without the constant offset term.

The final expansion can be simplified into the following form:

where mn is the multiplier resulting from the conversion of prefixes into scale factors according to the Table 3 and simplification, and un and en are the units name and corresponding exponent for the n-th base units.

Some examples of the expansion of units definitions will be made available soon.

5.5.5  Rules for equation dimension checking

If software chooses to verify that equations are self-consistent with respect to the dimensions of the units definitions referenced by all numbers and variables, it must obtain the same results as would be obtained by following these steps:

1. The equation is split into a tree of equation parts, in which each parent part is obtained by the application of a single operator to its children. A relational operator (typically the equals operator) combines the nodes at the top of the tree. An example of the tree formulation of an equation is given in Section 5.3.2. This specification will not attempt to further define this step.

2. The units definitions for the terms at the leaves of the tree are expanded into functions of the SI and user-defined base units. The expansion of a units definition into base units is discussed in Section 5.5.4.
3. Starting at the leaves of the tree, sets of child nodes can be recursively removed from the tree according to the operator applied to them. Operators such as addition or subtraction require that all of the child nodes have unit definitions with identical dimensions, as defined in Section 5.5.3. If this is true, the parent node assumes the same dimensions as its children. If it is not, the equation has inconsistent dimensions. There are no restrictions on the units definitions used by nodes combined using operators such as multiplication or division operators. The dimensions of the parent term assume the result of the appropriate operation on the dimensions of the child terms.
4. The equation has self-consistent dimensions if the fully expanded units definitions of the two nodes at the top of the tree are equivalent, as defined in Section 5.5.3.
5. It an inconsistency is detected at any point, then software is free to do whatever it likes. This specification recommends that it alert the user to a possible error, at the very least.

5.5.6  Units and variable mapping

If software claims to be able to perform units conversion when passing the value of a variable between components, it is required to produce results that are consistent with those that would be obtained using the algorithm described in this section.

If two variable declarations both reference identical units definitions as defined in Section 5.5.2, then there is a one-to-one mapping between the the variable's value in both components.

If two variable declarations reference different units definitions, some sort of units analysis and conversion is required to ensure that the model functions properly. If software chooses to perform this variable mapping, then it must be capable of converting any value of a variable x which is measured in U1 units to an equivalent value y measured in U2 units. This conversion must obtain the same results as would be obtained by following the procedure outlined below to derive a mathematical expression relating x to y:

1. Two mathematical expressions are generated, in which U1 and U2 are functions of SI and user-defined base units. The method by which these expressions are generated is discussed in Section 5.5.4.
2. U1 and U2 must have equivalent dimensions as defined in Section 5.5.3.
3. The expression relating U1 to the base units is inverted, and combined with the expression for U2 to give a single expression relating x to y. This inversion and substitution process is discussed in Section 5.5.7.

5.5.7  Generating an equation relating units definitions

The recursive resolution of units definitions according to the procedure defined in Section 5.5.4 leaves two equations that are of one of the following two forms:

In most cases, both equations will be of the same form. If the expressions for U1 and U2 are of different forms, the two equations will only have equivalent dimensions if the expression of form shown in Equation 2 has a single base unit u1, and e1 has a value of one.

The expanded equations for U1 and U2 can be related by either un, if the expressions are of the form shown in Equation 1, or by the product u1e1 ... unen, if the equations are of the form shown in Equation 2. The equation for x can be inverted. This inversion will result in one of the forms shown below:

The inverted equation for x can be substituted into the equation for y to give a single equation defining y in terms of x. Examples of this procedure will be made available soon.

6  Grouping

6.1  Introduction

It is often useful to organise groups of components within a model into a hierarchical structure. This structure might reflect the logical organisation of components within the group or their physical configuration. CellML provides a single mechanism for the specification of both of these forms of hierarchy. This mechanism is based on a grouping scheme that allows model authors to create numerous hierarchical structures over a single network of components. The parent-child relationships in one hierarchical grouping need not necessarily be consistent with those specified in another grouping, a situation that could not be supported by nesting of component definitions.

It is anticipated that models will typically be defined as a network, with hierarchical relationships defined between groups of components at different places within the model. CellML processing software is free to treat these structures as discontinuous. Alternatively, it may combine structures that represent the same relationship into a single hierarchy by assuming that the root nodes of any hierarchical arrangements of components are all children of a single imaginary component. This imaginary component is not explicitly defined within the CellML document and has no properties.

The definition of a logical hierarchy of components in a network is known as "encapsulation". Encapsulation allows the modeller to hide a group of components from the rest of the model by using a single component as an interface to the hidden subnetwork. The parent component hides the details of one or more child components from the rest of the model. Encapsulation provides a powerful mechanism for simplifying the structure of the model by preventing connections between specified sets of components. Components in the main network may not connect to the child components in the subnetwork — all variables must be mapped through the parent interface component. Components in the subnetwork may only be connected to the interface component and to other components in the same subnetwork, which may include further levels of encapsulation. Therefore, a modeller wishing to re-use an encapsulated subnetwork may treat the subnetwork as a "black box", and deal exclusively with the interface presented by the encapsulating component.

The definition of physical hierarchies within a model is known as "containment" in CellML. A model author can specify that one or more child components are physically inside of a parent component without describing the geometric aspects of the relationship in detail. This information would typically be used by CellML processing software to provide simple renderings of a model.

Model authors are also free to extend the grouping scheme with user-defined types of relationships between components. However, CellML processing software is only expected to recognise encapsulation and containment relationships.

Groups do not add any additional mathematical information to the model. Model authors may not define their own grouping relationships that are intended to imply mathematical information.

6.2  Basic Structure

6.2.1  Definition of groups

Logical and physical hierarchies are both declared using the <group> element. This element must be a child of a <model> element. Each <group> element contains one or more <relationship_ref> elements, each of which defines a relationship attribute, the value of which references the type of relationship represented by the group. CellML processing software is expected to recognise two types of relationship: encapsulation and containment, which are indicated by relationship attribute values of "is_encapsulated_by" and "is_contained_in", respectively.

The <group> element also contains two or more <component_ref> elements, each of which defines two attributes. The component attribute references a component within the current model. The role attribute indicates whether the component is the dominant component in the hierarchy. A component referenced by a <component_ref> element with a role attribute value of "major" is the dominant component. This component is the encapsulating component in a logical encapsulation hierarchy or the containing component in a geometric containment hierarchy. A <group> element contains one or more <component_ref> elements with a role attribute value of "minor". The components referenced by these elements are the encapsulated components in a logical encapsulation hierarchy or the contained components in a geometric containment hierarchy. A <group> element that defines a logical encapsulation or geometric containment relationship must reference exactly one major component and at least one minor component. A group element that defines a user-defined type of relationship may have any number of minor and major components.

A single <group> element may be used to define multiple relationships between components. For instance, encapsulation and geometric relationships may be defined within the same <group> element and thus share the same hierarchy. This is done by including more than one <relationship_ref> element in the <group> element. Each <relationship_ref> element must define a relationship attribute, which may be in the CellML namespace or in an extension namespace. The value of the relationship attribute names the type of relationship referenced by the <relationship_ref> element. If the relationship attribute is in the CellML namespace, its value must be either "is_encapsulated_by" or "is_contained_in". A <relationship_ref> element may also define a name attribute. The value of the name attribute on <relationship_ref> elements can be used to combine several <group> elements into a single hierarchical structure (see Section 6.2.4 for more information on this).

Geometric containment relationship information is formally independent of logical encapsulation information, but CellML processing software is free to check for inconsistencies between the two relationships — it would generally not be useful for an encapsulating component to be physically inside one of its encapsulated child components.

All children of a given major component in a single hierarchy must appear within a single <group> element. This simplifies the construction and validation of hierarchies from <group> elements. For instance, the requirement that a component may only have a single parent in any given hierarchy would be difficult to enforce if minor components could be scattered across several <group> elements.

6.2.2  The encapsulation relationship

Encapsulation allows the modeller to split a model into layers of complexity. A single component can be used to encapsulate a complex partial model, and thereby provide a unified interface for all information passing between that subnetwork and the rest of the model.

A model may only define a single encapsulation hierarchy, which may be continuous or discontinuous. Each component in the hierarchy may have at most one parent component. If the hierarchy is continuous, the parent component will always be another component defined within the current model. If the hierarchy is discontinuous, it may be convenient to assume that any unencapsulated components are children of a single imaginary component. This imaginary component makes it easier to check that the hierarchy has no circular relationships between components.

The components in a model can be divided into four sets with respect to any given component (the current component). The set of all components immediately encapsulated by the current component is the encapsulated set. The parent component is the component that encapsulates the current component. Other components encapsulated by the same parent make up the sibling set. All other components, which are not available to make connections with the current component, make up the hidden set. If the current component is not encapsulated, then it has no parent and the sibling set consists of all other unencapsulated components in the model.

These sets are best demonstrated by example. Given the network shown in Figure 10, Table 4 lists the parent components and the components in the encapsulated, sibling, and hidden sets for a selected set of components picked as the current component.

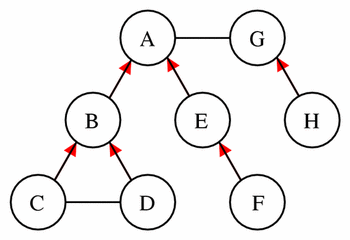
Figure 10 This simple model provides the basis for the demonstration of the concepts of encapsulated sets, parents, sibling sets, and hidden sets, as described in the text. The model consists of eight components each represented by a circle. The lines between the components represent connections, and a red arrowhead on one of these lines indicates that the component at the tail of the arrow is encapsulated by the component at the head of the arrow.

Table 4 This table lists the parent components, and the components in the encapsulated, sibling, and hidden sets for a selected few components from the example model in Figure 10. Components A and G do not have a real parent component, but may have an imaginary parent component that enables the formation of a single encapsulation hierarchy.

Every variable must define its availability for use in other components. This is done with the public_interface and private_interface attributes on the <variable> element. The interface exposed to the parent component and components in the sibling set is defined by the public_interface attribute. The private_interface attribute defines the interface exposed to components in the encapsulated set. Each interface has three possible values: "in", "out", and "none", where "none" indicates the absence of an interface. The separation of interfaces allows the modeller to incrementally add complexity to a encapsulated network without changing the interface presented to the rest of the network by the encapsulating component.

The mappings that are allowed between variables declared in each component are controlled by the public and private interfaces of each variable and the prohibition on connecting an encapsulated component to components other than its parent component, members of its sibling set, and any components it in turn encapsulates. Variables with a public_interface attribute value of "in" must be mapped to a single variable in the sibling set with a public_interface attribute value of "out" or to a single variable in the parent of the current component with a private_interface attribute value of "out". Similarly, variables with a public_interface value of "out" may be mapped to variables in components in the sibling set with a public_interface attribute value of "in" or to variables in the parent component with a private_interface value of "in". Note that defining a public_interface attribute value of "out" on a variable makes it legal to map the variable to other variables, but does not require that such a mapping occur. If a variable has a public_interface attribute value of "none", it cannot be mapped to variables in the parent component or to variables in components in the sibling set.

Variables with a private_interface attribute value of "in" must be mapped to a single variable from a single component in the encapsulated set with a public_interface attribute value of "out". Variables with a private_interface attribute value of "out" may be mapped to any variables from components in the encapsulated set with a public_interface attribute value of "in". If a variable has a private_interface attribute value of "none", it is neither input from or exposed to the components in the encapsulated set.

If both the public_interface and private_interface attributes of a variable have a value of "none", the variable can only be used in the current component and is invisible to all other components in the model. In order to determine which variables may be modified in the current component, we must determine if either the public_interface attribute or the private_interface attribute has a value of "in". If so, the variable is declared elsewhere and its value may not be mathematically modified in the current component. If not, the variable belongs to the current component.

The two interface attributes of a variable are completely independent with one exception: it is invalid for a variable to have both public_interface and private_interface attributes with value "in". An interface with value "in" reflects an unmet need in the current component that must be satisfied — this need can be met in either the public or private interface, but not both.

6.2.3  The containment relationship

The is_contained_in relationship allows the modeller to specify that a particular component is physically inside another. This might be used by software for the rendering of a model. Containment relationships can be specified either in combination with or independent of encapsulation relationships. Containment relationships do not restrict any aspect of model definition or behaviour.

6.2.4  Named containment hierarchies

CellML allows the definition of multiple containment hierarchies over the same network model. This functionality allows the modeller to define several different ways of organising the same model, each of which might highlight a different aspect of the model's physical structure. This functionality has been included in CellML for extended compatibility with AnatML, an XML-based language for describing anatomical structures.

A containment hierarchy is created when several <group> elements contain <relationship_ref> elements with a relationship attribute value of "is_contained_in" and the same name attribute value. Any <group> elements that contain <relationship_ref> elements with a relationship attribute value of "is_contained_in" and that do not define a name attribute are also considered to form a single grouping hierarchy.

As was the case for encapsulation grouping, a containment hierarchy may be continuous or discontinuous. Each component in the hierarchy may have at most one parent component. If the hierarchy is continuous, the parent component will always be another component defined within the current model. If the hierarchy is discontinuous, it may be convenient to assume that any components not already contained within other components are children of a single imaginary component. This imaginary component makes it easier to ensure that the hierarchy has no circular relationships between components.

6.2.5  User-defined relationship types

Modellers are free to use the grouping syntax of CellML to organise model components in ways not described in the CellML specification. To do this, the model author defines a new relationship type, the name of which is used as the value of the relationship attribute on the <relationship_ref> element. The relationship attribute must be placed in an extension namespace, because future versions of the CellML specification may define additional relationship types, the names of which could otherwise conflict with user-defined relationship types. If a modeller uses a non-standard value for the relationship attribute, the value used should indicate the relationship between minor and major components. A <group> element that defines a user-defined type of group is free to contain only minor components. For example, a modeller may define a grouping class called "is_next_to", used to tell a processor that one minor component is physically adjacent to another.

Modellers are free to use the name attribute on the <relationship_ref> element to specify multiple hierarchies for user-defined relationship types, as is possible for the containment relationship.

This specification does not provide a mechanism by which modellers may specify the meaning of a user-defined type of relationship. This definition must be provided by the processing software declaring the new relationship type.

6.3  Examples

Figure 11 demonstrates the use of the <group> element to define an encapsulation relationship. This example is taken from the two reaction pathway with encapsulation example from the examples section of the CellML website. It shows how a component representing an overall reaction (total_reaction) can encapsulate components representing intermediate reactions (first_reaction and second_reaction) and their by-products (C and D).

<group>
  <relationship_ref relationship="is_encapsulated_by" />
  <component_ref component="total_reaction" role="major" />
  <component_ref component="first_reaction" role="minor" />
  <component_ref component="second_reaction" role="minor" />
  <component_ref component="C" role="minor" />
  <component_ref component="D" role="minor" />
</group>

Figure 11 Example demonstrating the use of the <group> element to define a logical encapsulation relationship. See text for more details.

Figure 12 demonstrates the use of the <group> element to define encapsulation and containment relationships, the construction of two named geometric hierarchies, and the specification of a custom relationship type (is_next_to) in an extension namespace. Most CellML models will probably only define a single geometric hierarchy. In this case, it is not necessary to name the hierarchy, since all unnamed groups are assumed to belong to the same geometric hierarchy.

<group>
  <relationship_ref name="membrane" relationship="is_contained_in" />
  <component_ref component="cell" role="major" />
  <component_ref component="cell_membrane" role="minor" />
</group>

<group>
  <relationship_ref relationship="is_encapsulated_by" />
  <relationship_ref name="membrane" relationship="is_contained_in" />
  <component_ref component="cell_membrane" role="major" />
  <component_ref component="sodium_channel" role="minor" />
  <component_ref component="calcium_channel" role="minor" />
</group>

<group>
  <relationship_ref name="intracellular" relationship="is_contained_in" />
  <component_ref component="cell" role="major" />
  <component_ref component="network_sarcoplasmic_reticulum" role="minor" />
  <component_ref component="junctional_sarcoplasmic_reticulum" role="minor" />
</group>

<group>
  <relationship_ref
      app:relationship="is_next_to"
      xmlns:app="http://www.software.com/cellml_processor" />
  <component_ref component="network_sarcoplasmic_reticulum" role="minor" />
  <component_ref component="junctional_sarcoplasmic_reticulum" role="minor" />
</group>

Figure 12 Examples demonstrating the use of the <group> element. See text for more details.

The first <group> element states that the cell_membrane component is physically inside the cell component, and that this geometric relationship is part of a geometric hierarchy called membrane. The second <group> element states that the sodium_channel and calcium_channel components are both physically inside and logically encapsulated by the cell_membrane component. This completes the membrane geometric hierarchy. The encapsulation relationship prevents the sodium and calcium channel components from being connected to any components other than the cell_membrane component, each other, and any components they in turn encapsulate.

The third <group> element states that the two components representing parts of the sarcoplasmic reticulum are physically inside the cell, and that this relationship is part of a geometric hierarchy called intracellular. Finally, the fourth <group> element introduces the user-defined relationship is_next_to, and states that the the two sarcoplasmic reticulum components share this relationship. This relationship type is declared by putting the relationship attribute in an extension namespace, and assigning it a value of "is_next_to". Note that this relationship has no major or dominant component, and that CellML processing software is free to ignore the information provided by this group.

6.4  Rules for CellML Documents

6.4.1  The <group> element

1. Allowed use of the <group> element
   • A <model> element may contain any number of <group> elements.
   • A <group> element must contain only the following elements, which may appear in any order:
     • <relationship_ref> and <component_ref> elements in the CellML namespace,
     • metadata framework elements, as described in Section 8.
     [ Recommended practice is to define the CellML namespace child elements in a <group> element in the order stated above. ]
   • A <group> element must contain at least one <relationship_ref> element.
   • A <group> element must contain at least one <component_ref> element.

6.4.2  The <relationship_ref> element

1. Allowed use of the <relationship_ref> element
   • A <relationship_ref> element must contain only the following elements, which may appear in any order:
     • metadata framework elements, as described in Section 8.
   • Each <relationship_ref> element must define a relationship attribute in either the CellML namespace or an extension namespace. It may also define a name attribute. [ A relationship attribute declaring a user-defined relationship type is placed in an extension namespace. This prevent conflicts with future versions of the CellML specification, which may define additional types of relationships in the CellML namespace. ]
2. Allowed values of the relationship attribute
   • The value of a relationship attribute in the CellML namespace must be "is_contained_in" or "is_encapsulated_by".
3. Allowed values of the name attribute
   • The value of the name attribute must be a valid CellML identifier as discussed in Section 2.2.1. [ Note that unlike most other name attributes, the value of the name attribute on a <relationship_ref> element is not expected to be unique across the current model. Instead, <group> elements that include <relationship_ref> elements that share the same name attribute value form are parts of a single hierarchy. ]
4. Proper use of the name attribute
   • A name attribute may not be defined on a <relationship_ref> element with a relationship attribute value of "is_encapsulated_by". [ A model may define only a single, unnamed encapsulation hierarchy. ]

6.4.3  The <component_ref> element in <group> elements

1. Allowed use of the <component_ref> element within a <group> element
   • A <component_ref> element must contain only the following elements, which may appear in any order:
     • metadata framework elements, as described in Section 8.
   • A <component_ref> element within a <group> element must define a component attribute and a role attribute.
2. Proper use of the <component_ref> element in <group> elements
   • Two <group> elements that contain <relationship_ref> elements with identical relationship attribute values and undefined name attributes may not reference the same major component. [ A single level of a hierarchy must only be defined with a single <group> element. It would be much more difficult to assemble a hierarchy from a CellML document if a single level of the hierarchy could be shared among multiple <group> elements. ]
   • Two <group> elements that contain <relationship_ref> elements with identical relationship and name attribute values may not reference the same major component. [ This rule extends the previous rule to include named hierarchies. ]
   • A component must not be referenced as a minor component more than once in a single grouping hierarchy. All <component_ref> elements with a common component attribute value and a role attribute value of minor must be in different hierarchies. [ A grouping hierarchy must not be circular. ]
3. Allowed values of the component attribute
   • The value of the component attribute must equal the value of the name attribute of a <component> element contained within the current <model> element.
   • The value of the component attribute on a <component_ref> element must be unique across all <component_ref> elements within the parent <group> element. [ A component may only appear once within a group. ]
4. Allowed values of the role attribute
   • The value of the role attribute on a <component_ref> element in a <group> element must be either "major" or "minor".
5. Proper use of the role attribute
   • A <group> element that contains a <relationship_ref> element with a relationship attribute of "is_encapsulated_by" or "is_contained_in" must contain exactly one <component_ref> element with a role attribute value of "major" and at least one <component_ref> element with a role attribute value of "minor". [ Groups defining an encapsulation or containment relationship must have exactly one dominant component and at least one minor component. ]

6.5  Rules for Processor Behaviour

6.5.1  Allowing multiple grouping hierarchies in a single model

A given model may define multiple geometric containment hierarchies, but may only define one logical encapsulation hierarchy.

A grouping hierarchy is built up from multiple <group> elements based on the value of the name attribute of the <relationship_ref> elements. All <group> elements that contain <relationship_ref> elements that share the same relationship and name attribute values are considered to form a single grouping hierarchy. All <group> elements that contain <relationship_ref> elements that share the same relationship attribute value and do not define name attributes are also considered to form a single grouping hierarchy.

If, after the groups that make up a single hierarchy are assembled, the resulting hierarchy is discontinuous, it may be convenient to assume that any components that are not already children of other components are children of a single imaginary component. The imaginary component has no properties in the model. Its sole purpose is to make it easier to check that the hierarchy has no circular relationships between components.

6.5.2  Groups must not imply mathematical information

Modellers are explicitly forbidden from using CellML groups to add mathematical information to the model. Modellers may not define their own types of relationships that imply mathematics.

6.5.3  Groups should not imply metadata information

Modellers should not use CellML groups to associate properties or classification information with sets of components. The metadata functionality is the proper method for making such associations. This increases the chance of that information being used by a range of CellML processing software.

7  Reactions

7.1  Introduction

CellML is intended to be used to represent many different types of models. Therefore, its basic structure is rather general, and models are primarily specified by explicitly defining mathematics using MathML. It will always be possible to specify a model purely in terms of mathematics, without using any of the elements defined in this section of the specification. However, in some types of models, information is lost in reducing the model to pure mathematics. For instance, in biochemical pathway models it will not always be straightforward, or even possible, to unambiguously determine from the mathematical rate laws which variables represent inhibitors or activators in the reactions. Therefore, some additional elements were needed in CellML to fully capture the information in biochemical pathway models.

7.1.1  Pathway model representations supported by CellML

Three fundamental representations of reaction/pathway models must be supported by CellML:

• Mathematical Equations: these are any valid mathematical equations that describe the model. For example, they may be ordinary differential equations that define kinetic reaction rate laws and the rate of change of the concentration of species participating in the modelled reactions.
• Chemical Expressions: these are the stoichiometric expressions (such as A + B <-> 2C + D) used by chemists to represent reactions.
• Pathway Diagrams: these are the stylised drawings commonly used by biochemists and cell biologists to represent interactions among participants in reactions. Some examples of pathway diagrams are shown in Section 7.3.

It is important that CellML be able to store the information needed to unambiguously reproduce any of these representations of a model. It is also important to minimise duplication of information within the model definition, because duplication can lead to inconsistencies. Therefore, we must integrate the information needed to support the three types of model representation.

The integration process has resulted in the introduction of a CellML syntax that implies a mathematical relationship between variables in the current component. In this section of the specification, explicit mathematics refers to equations defined using MathML, and implicit mathematics refers to equations implied from the CellML syntax.

7.1.2  Qualitative vs. quantitative pathway models

CellML supports both quantitative and qualitative pathway models. Many types of models are commonly referred to as "qualitative". Some of these are mathematically specified, while others are not. For the purposes of this specification, qualitative pathway models consist solely of information about how the different chemical species in the pathway relate, and contain no mathematics. However, the stoichiometry of the reactions may be known. In other words, there is no mathematical representation of the model, but there may still be a pathway diagram and chemical expressions that represent the model. Because there is no mathematics in a qualitative model, CellML processing software is not required to be able to run a simulation using a qualitative model. However, some software may support simple simulations using such models.

Any model in which the change of concentration of a chemical species participating in a reaction is implicitly or explicitly defined is quantitative. All others are qualitative.

7.2  Basic Structure

The <reaction> element is used to store information associated with a single reaction. It may only appear inside of a <component> element. Examples of the <reaction> element are shown in Section 7.3. It is possible for a single <component> element to contain more than one <reaction> element. However, this practice makes it more difficult to re-use the individual reactions, and is therefore not recommended. The <reaction> element may define a reversible attribute, the value of which indicates whether or not the reaction is reversible. The default value of the reversible attribute is "yes".

The reaction element contains multiple <variable_ref> components, each of which references one of the variables that participates in the reaction. The recommended practice is to create a <variable_ref> element for each variable representing the concentration of a chemical species that participates in a reaction, as well as one for the variable representing the rate of the reaction. The required variable attribute is the only attribute on the <variable_ref> element. Its value is the name of the referenced variable. This variable must be declared in the current <component> element.

Each <variable_ref> element contains one or more empty <role> elements. There are four possible attributes on the <role> element. The required role attribute specifies the way in which the variable participates in the reaction. There are currently seven values allowed for this attribute: "reactant", "product", "catalyst", "activator", "inhibitor", "modifier", and "rate". These are defined in Section 7.4. The optional direction attribute should only be used on <role> elements in reversible reactions. It may have values of "forward", "reverse", or "both" and indicates the direction of the reaction for which the role is relevant. It has a default value of "forward". The optional delta_variable attribute indicates which variable is used to store the change in concentration of the species represented by the variable referenced by the current <variable_ref> element. The optional stoichiometry attribute stores the stoichiometry of the current variable relative to the other reaction participants. Section 7.4 contains detailed rules for the use of these attributes.

The <role> elements may also contain <math> elements, which define equations using MathML. Although it is not required, it is recommended practice to store all of the equations that relate to a reaction inside the appropriate <role> elements in the <reaction> element. This makes the <reaction> element more re-usable. In addition, defining mathematics inside a <role> element has the effect of associating the equations with the variable referenced by the containing <variable_ref> element, in the role defined by the <role> element. This enables CellML processing software to present the equations in a more meaningful context. For instance, it might group all of the relationships between the rate variable and the delta variables for all of the reactants and products, or it might display these equations in a different color. (Note that CellML processing software is not required to provide such additional functionality.)

There are three uses for equations inside <role> elements:

• If the role attribute value is "rate", any enclosed equations calculate the kinetic rate law (i.e., calculate the value of the referenced variable) and the value of intermediate variables used in the rate law equation.
• If the role attribute value is "reactant" or "product", the equations calculate the relationship between the general reaction rate and the rate of change of the species represented by the referenced variable (i.e., calculate the value of the variable named in the delta_variable attribute), and calculate any intermediate variables used in this relationship.
• In all other cases, the equations relate an intermediate variable used in the rate calculation to the variable referenced by the containing <variable_ref> element. For instance, it would be appropriate to calculate an effective concentration of a catalyst inside the <role> element contained by the <variable_ref> element that references the variable representing the actual concentration of the catalyst.

Note that CellML processing applications are not required to be able to deduce the stoichiometry of a reaction from explicit mathematics. Therefore, it is strongly recommended that the stoichiometry and delta_variable attributes be used instead of explicit mathematics if the concentration change is simply the reaction rate multiplied by the stoichiometry. (The rules for deriving this mathematical relationship from the stoichiometry attribute are defined in Section 7.5.3.)

7.3  Examples

This section contains two examples demonstrating the recommended use of the <reaction> and <role> elements to define two basic reactions. The mathematics defining the reaction rate have been omitted in these examples. See the reaction model examples section of the CellML website for further examples.

Figure 13 shows a pathway diagram representation of the following reversible reaction:

Figure 14 demonstrates the use of CellML to define this reaction. There are five <variable_ref> elements in the <reaction> element: one for each variable representing the concentration of a chemical species participating in the reaction, and one for the variable representing the general reaction rate. Note that the stoichiometry attribute has a value of "2" for the variable representing the chemical species C, since this species appears with a stoichiometry of 2 in the chemical expression. The reversible attribute on the <reaction> element and the direction attributes on the <variable_ref> elements have their default values ("yes" and "forward", respectively) and therefore could have been omitted. They are included for clarity.

Figure 13 A typical pathway diagram representation of the simple reversible reaction A + B <-> 2C + D.

<reaction reversible="yes">
  <variable_ref variable="A">
    <role
        role="reactant" direction="forward"
        delta_variable="delta_A" stoichiometry="1" />
  </variable_ref>

  <variable_ref variable="B">
    <role
        role="reactant" direction="forward"
        delta_variable="delta_B" stoichiometry="1" />
  </variable_ref>

  <variable_ref variable="C">
    <role
        role="product" direction="forward"
        delta_variable="delta_C" stoichiometry="2" />
  </variable_ref>

  <variable_ref variable="D">
    <role
        role="product" direction="forward"
        delta_variable="delta_D" stoichiometry="1" />
  </variable_ref>

  <variable_ref variable="r">
    <role role="rate">
      <math xmlns="http://www.w3.org/1998/Math/MathML">
        ...  <!-- reaction rate math -->
      </math>
    </role>
  </variable_ref>
</reaction>

Figure 14 The CellML definition of the simple reversible reaction A + B <-> 2C + D. See text for more details.

Figure 15 shows the pathway diagram for the following irreversible, catalyzed reaction, which exhibits product-inhibition:

The CellML definition of this reaction is shown in Figure 16.

Figure 15 A typical pathway diagram representation of the irreversible reaction A + B -> D (catalyzed by C, inhibited by D).

<reaction reversible="no">
  <variable_ref variable="A">
    <role role="reactant" delta_variable="delta_A" stoichiometry="1" />
  </variable_ref>

  <variable_ref variable="B">
    <role role="reactant" delta_variable="delta_B" stoichiometry="1" />
  </variable_ref>

  <variable_ref variable="C">
    <role role="catalyst" />
  </variable_ref>

  <variable_ref variable="D">
    <role role="product" delta_variable="delta_D" stoichiometry="1" />
    <role role="inhibitor" stoichiometry="1" />
  </variable_ref>

  <variable_ref variable="r">
    <role role="rate">
      <math xmlns="http://www.w3.org/1998/Math/MathML">
        ...  <!-- reaction rate math -->
      </math>
    </role>
  </variable_ref>

</reaction>

Figure 16 The CellML definition of the irreversible reaction A + B -> D (catalyzed by C, inhibited by D). See text for more details.

The <variable_ref> element that references the variable representing the concentration of species D now contains two <role> elements, one with information about D as a product and the other with information about D as an inhibitor. In this example, D has the same stoichiometry in both roles, but this would not necessarily need to be the case.

7.4  Rules for CellML Documents

7.4.1  The <reaction> element

1. Allowed use of the <reaction> element
   • A <component> element may contain any number of <reaction> elements. [ The use of multiple <reaction> elements within a single <component> element is discouraged, but is not illegal. ]
   • A <reaction> element must contain only the following elements, which may appear in any order:
     • <variable_ref> elements in the CellML namespace,
     • metadata framework elements, as described in Section 8.
     [ The recommended practice is to define one <variable_ref> element for each variable representing a chemical species that participates in the reaction, and one <variable_ref> element for the variable representing the rate of the reaction. ]
   • The <reaction> element may define a reversible attribute.
2. Allowed values of the reversible attribute
   • If present, the reversible attribute must have a value of "yes" or "no".
   • If not present, its value defaults to "yes". [ It is recommended to always explicitly define the value of this attribute. ]
3. Proper use of the <reaction> element in encapsulating components

   [ It is often convenient to include a <reaction> element in a component that is encapsulating several intermediate reactions (see Section 6 for more information about encapsulation). The encapsulating component represents an overall, or total, reaction, which can be represented by a <reaction> element. This total reaction is effectively qualitative, because any mathematics representing the progression of the total reaction is defined in the components representing the intermediate reactions. ]

   • A <reaction> element in an encapsulating component may not contain delta_variable attributes on the <role> elements or explicit mathematics defining the overall reaction rate or the changes in concentration of the species that participate in the total reaction. [ A valid CellML model must not define an inconsistent set of equations. Therefore, one should not introduce explicit or implicit mathematics in an encapsulating component that duplicates or contradicts mathematics (either explicit or implicit) defined in the encapsulated components. ]

7.4.2  The <variable_ref> element within a <reaction> element

1. Allowed use of the <variable_ref> element within a <reaction> element
   • A <variable_ref> element in a <reaction> element must contain only the following elements, which may appear in any order:
     • <role> elements in the CellML namespace,
     • metadata framework elements, as described in Section 8.
   • Each <variable_ref> element within a <reaction> element must contain at least one <role> element. [ The recommended best practice is to define one <role> element for each role assumed by the chemical species represented by the referenced variable. ]
   • Each <variable_ref> element within a <reaction> element must define a variable attribute.
2. Allowed values of the variable attribute
   • The value of the variable attribute on a <variable_ref> element within a <reaction> element must equal the value of the name attribute on a <variable> element defined inside the current <component> element.
   • The value of the variable attribute must be unique across all <variable_ref> elements contained within the parent <reaction> element. [ A variable may only be referenced once in a single reaction. ]

7.4.3  The <role> element

1. Allowed use of the <role> element
   • A <role> element must contain only the following elements, which may appear in any order:
     • <math> elements in the MathML namespace,
     • metadata framework elements, as described in Section 8.
     [ Some rules for the use of mathematics in <role> elements are provided below, and rules for the <math> element and its children are given in Section 4. ]
   • Each <role> element must define a valid role attribute value. It may also define direction, delta_variable, and stoichiometry attributes, subject to the constraints specified in the subsequent sections.
2. Allowed values of the role attribute
   • The role attribute must take one of the following seven values:
     • "reactant": the species represented by the referenced variable is one of the species consumed or transformed by the reaction (in the forward direction). Reactants are also often called substrates.
     • "product": the species represented by the referenced variable is one of the species produced by the reaction (in the forward direction).
     • "catalyst": the species represented by the referenced variable catalyzes the reaction. In biochemical pathways, such a species will almost always be an enzyme and will almost always occur with a stoichiometry attribute value of "1".
     • "activator": the species represented by the referenced variable enhances the reaction. Activators can occur with any stoichiometry. An activator will usually be a small molecule that increases the activity of an enzyme catalyzing the reaction. However, the detailed reaction representing this activation of the enzyme may not be included in the model. Instead, the activator may be represented as directly affecting the kinetics of the catalyzed reaction.
     • "inhibitor": the species represented by the referenced variable inhibits the reaction. Inhibitors can occur with any stoichiometry. An inhibitor will usually be a species that inhibits the activity of an enzyme catalyzing the reaction. However, the detailed reaction representing this inhibition of the enzyme may not be included in the model. Instead, the inhibitor may be represented as directly affecting the kinetics of the catalyzed reaction.
     • "modifier": the species represented by the referenced variable modifies the reaction in some unspecified way.
     • "rate": the referenced variable represents the rate of the reaction.
3. Proper use of the role attribute
   • Only one <variable_ref> element in a given <reaction> element can contain a <role> element with a role attribute with a value of "rate". [ There may only be one rate variable per reaction. ]
   • A <variable_ref> element that contains a <role> element with a role attribute value of "rate" must not contain other <role> elements. [ The variable assigned the "rate" role may not be assigned any other roles. ]
   • A <role> element with a role attribute of "rate" may not also define direction, delta_variable, or stoichiometry attributes. [ The reaction rate should always be defined in the forward direction. To do otherwise will cause the implicit mathematics defined by the delta_variable and stoichiometry attributes of the reactant and product roles to be erroneous. The delta_variable and stoichiometry attributes have no meaning for a rate variable. ]
   • If a <role> element has a role attribute value of "reactant", there must be no other <role> element within the same parent <variable_ref> element with a role attribute value of "product". [ A species may not be explicitly defined to be both a product and a reactant, although this is implied by a reversible reaction. ]
4. Allowed values of the direction attribute
   • If present, the direction attribute must take one of the following three values:
     • "forward": the value of the role attribute is the role of the referenced variable in the reaction when running in the "favoured" direction. The favoured direction is the one in which the the reactants are being consumed (i.e., the time-derivatives of their concentrations are negative), as defined by the kinetic rate law.
     • "reverse": the value of the role attribute is the role of the referenced variable in the reaction when running opposite to the "favoured" direction. In this direction, the reactants (as defined by the kinetic rate law) are being produced.
     • "both": the value of the role attribute is the role of the referenced variable in both directions of the reaction.
   • If not present, the value of the direction attribute defaults to "forward".
5. Proper use of the direction attribute
   • A direction attribute must only be defined on <role> elements contained in a <reaction> element on which the reversible attribute has a value of "yes". [ Only reversible reactions may occur in two directions. ]
   • The direction attribute on a <role> element for which the role attribute has a value of "reactant" or "product" must only have a value of "forward". [ This prevents the definition of inconsistent chemistry that could occur if a species could be explicitly defined as both a reactant and a product. ]
   • The direction attribute must only assume the value of "both" on <role> elements with a role attribute value of "catalyst", "activator", "inhibitor", or "modifier". [ It is not chemically sensible to say that a species is a "reactant" in both directions. Nor does it make sense to declare that a species is a "product" in both directions. ]
   • Each <role> element contained in a given <variable_ref> element must have a unique combination of values for the role and direction attributes. [ Defining two <role> elements with the same role and direction attribute values would allow the definition of inconsistent stoichiometries or multiple delta variables for a single variable. Both of these situations would create invalid CellML. ]
6. Allowed values of the stoichiometry attribute
   • If present, the value of the stoichiometry attribute must be a real number. [ In most cases, the value will be an integer. However, a valid CellML model may use fractional stoichiometries. ]
   • The absence of a stoichiometry attribute formally implies nothing. [ The absence of a stoichiometry value specifically does not imply a stoichiometry of "1". Instead, it would usually mean that the stoichiometry of the reaction is unknown. ]
7. Allowed values of the delta_variable attribute
   • If present, the value of the delta_variable attribute must equal the name attribute on a <variable> element defined inside the current <component> element.
   • The absence of the delta_variable attribute implies nothing.
   • The value of the delta_variable attribute must be unique across all <role> elements contained within the parent <component> element. [ One variable cannot represent the rate of change in concentration of more than one species. The value of the delta_variable attribute must be unique across the entire <component> element because it is legal (but not recommended) to include more than one <reaction> element in a single component. ]
8. Proper use of the delta_variable attribute
   • The delta_variable attribute may only appear on <role> elements in which the role attribute equals "reactant" or "product". [ It is only in these roles that a chemical species may undergo a change in concentration. ]
   • A <role> element on which a delta_variable attribute is declared must also either declare a stoichiometry attribute or include at least one <math> element in the MathML namespace. [ The combination of the delta_variable attribute and the stoichiometry attribute implies a mathematical relationship between the variable referenced in the delta_variable attribute and the variable assigned the role of "rate", as defined in Section 7.5.3. If the stoichiometry attribute is absent, the relationship between the variable named in the delta_variable attribute and the variable assigned the role of "rate" must be defined using MathML. ]
   • A <role> element on which the stoichiometry and delta_variable attributes are both defined must not also include <math> elements in the MathML namespace. [ The equations in a <math> element inside a <role> element for which the role attribute is "reactant" or "product" must relate the variable named in the delta_variable attribute to the variable assigned the role of "rate". Such equations would contradict the relationship implied by the delta_variable and stoichiometry attributes, as defined in Section 7.5.3. ]
   • If the delta_variable and stoichiometry attributes are both declared on any single reaction participant, a <variable_ref> element must be provided for the variable that represents the reaction rate. This <variable_ref> must contain exactly one <role> element, with a role attribute equal to "rate". [ Note that the reverse is not true: a variable may be assigned a role of "rate" even if the "reactant" and "product" variables do not define delta_variable attributes. In this case, the modeller may choose to provide explicit mathematics relating the "rate" variable to the change in concentration of the various chemical species. ]
9. Proper use of a <math> element inside a <role> element
   • A <math> element in the MathML namespace inside a <role> element must define equations that are relevant to the variable referenced by the containing <variable_ref> element, acting in the role defined by the role attribute on the <role> element. [ The meaning of "relevant" in this context is discussed in Section 7.5.4. ]

7.5  Rules for Processor Behaviour

7.5.1  Implications of the reversible attribute on the <reaction> element

If the reversible attribute has a value of "yes", it is assumed that all reactants in the forward direction are products in the reverse direction and vice versa. Similarly, all products in the forward direction are assumed to be reactants in the reverse direction and vice versa.

7.5.2  Chemical information implied by the stoichiometry attribute

The value of the stoichiometry attribute on a <role> element is defined to be the stoichiometry of the chemical species whose concentration is represented by the variable referenced by the containing <variable_ref> element. This stoichiometry can be used to produce the chemical expression representation of the model.

7.5.3  Math implied by the delta_variable and stoichiometry attributes

The use of the delta_variable and stoichiometry attributes on a <role> element implies the following mathematical relationship between the declared delta variable and the rate variable:

• For reactants: delta_variable = (stoichiometry)(rate)
• For products: delta_variable = -(stoichiometry)(rate)

The two reactions shown in Figure 17 are mathematically equivalent. The representation in the first reaction in Figure 17 is the recommended practice, because processing applications are not required to be able to extract the stoichiometry from an explicit MathML definition such as the one shown in the second reaction.

Explicit mathematics should only be used in cases where the implicit formulation would be inappropriate. Some examples of such cases are:

• If the stoichiometry of a reaction is unknown, but the modeller still wishes to relate the rate of change of a particular chemical species to the general reaction rate. Defining the stoichiometry attribute implies that the stoichiometry is known to equal the value of that attribute.
• If the modeller wishes to experiment with the stoichiometry of a species in different simulations using the model. (In this case, it might be easier if the stoichiometry is defined as a variable.)
• If the math implied from the recommended formulation would be incorrect, i.e., in the rare cases when a more complex function is needed to relate the change in concentration of a species to the reaction rate.

In all of these cases, it is recommended practice to put the mathematical expression used to define the change in concentration of a species inside the <role> element contained in the <variable_ref> element referring to the variable representing the concentration of that species.

<reaction reversible="yes">
  <variable_ref variable="A">
    <role
        role="reactant" direction="forward"
        delta_variable="delta_A" stoichiometry="1" />
  </variable_ref>

  ...
 
  <variable_ref variable="r">
    <role role="rate" />
    <math xmlns="http://www.w3.org/1998/Math/MathML">
       ...  <!-- reaction rate math -->
    </math>
  </variable_ref>
</reaction>

<reaction reversible="yes">
  <variable_ref variable="A">
    <role
        role="reactant" direction="forward"
        delta_variable="A" />
    <math xmlns="http://www.w3.org/1998/Math/MathML">
      <apply><eq />
        <ci> delta_A </ci>
        <apply><times />
          <cn cellml:units="dimensionless"> 1.0 </cn>
          <ci> r </ci>
        </apply>
      </apply>
    </math> 
      
  </variable_ref>

  ...
 
  <variable_ref variable="r">
    <role role="rate" />
    <math xmlns="http://www.w3.org/1998/Math/MathML">
       ...  <!-- reaction rate math -->
    </math>
  </variable_ref>
</reaction>

Figure 17 The top <reaction> element shows the recommended method for defining the change in concentration delta_A of a chemical species A with respect to the reaction rate r. The second <reaction> element shows an equivalent representation using an explicit MathML definition. Use of this formulation is not recommended. The MathML blocks defining the rate laws are omitted.

It is an error to explicitly declare mathematics that conflicts with or duplicates implied mathematics. Therefore, a modeller cannot declare a stoichiometry attribute and delta_variable attribute in addition to explicit math relating the change in concentration of the referenced species to the reaction rate.

7.5.4  Meaning of mathematics in reactions

Equations defined in <math> elements in the MathML namespace inside a <role> element must be relevant to the the variable referenced by the parent <variable_ref> element, acting in the role defined by the value of the role attribute. This means that:

• If the role attribute value is "rate", the equations must calculate the kinetic rate law (i.e., calculate the value of the referenced variable). Intermediate calculations related to the calculation of the rate are also allowed.
• If the role attribute value is "reactant" or "product", the equations must calculate the relationship between the general reaction rate and the rate of change of the species represented by the referenced variable (i.e., calculate the value of variable named in the delta_variable attribute). Intermediate calculations related to the calculation of the delta variable are also allowed.
• In all other cases, the equations must relate an intermediate variable used in the rate calculation to the variable referenced by the containing <variable_ref> element. For example, it would be appropriate to calculate an effective concentration of an inhibitor or catalyst in the <role> element contained in the <variable_ref> element that references the variable representing the actual concentration of that species.

7.5.5  Resolution of inconsistencies

Duplication of information is avoided as much as possible. However, because modellers must be free to define arbitrary rate laws, it was not possible to eliminate all information duplication. For instance, we cannot expect software to be able to deduce all information about a reaction from kinetic laws of arbitrary form, even though most information is in fact represented in these laws. Therefore, there is a possibility that the information in the mathematics and the information in the <reaction> element may be inconsistent.

It is anticipated that most modellers will define CellML models using some sort of processing software, which can reasonably be expected to write consistent CellML. However, since CellML is a text-based format, modellers may also create or edit models by hand, and in doing so risk creating inconsistent models.

The following rules govern the required behavior of CellML-compliant processing software in the event that information in the mathematics and the information in the reaction element do not agree:

• Preference is given to mathematics explicitly defined using MathML when running a simulation with the model.
• CellML processing software is free to determine which information to use in representing the model. Software is free to ignore the mathematics when creating a pathway diagram or chemical expression rendering of the model. However, software should clearly document which information is used to create representations of the model.
• Processing software may check for inconsistencies between the mathematics and the information in the <reaction> element. However, it is not required to do so, and it is left to the processing software to determine what to do if an inconsistency is found.

8  Metadata Framework

8.1  Introduction

Metadata is "data about data". In a CellML document, the principal data defined is the structure and mathematics of a biological model. Information that provides context for this data is metadata. Metadata can be included in a CellML document to facilitate searches of collections of models and model components. It provides a means for a modeller to include structured descriptive information about the model, which can help other modellers determine whether they can incorporate the model into their own work.

The CellML metadata structure is defined in a parallel document. This section of the CellML specification presents a framework for the use of metadata in a CellML document.

8.2  Basic Structure

Metadata is defined in a CellML document using the Resource Description Framework (RDF), which is a W3C recommendation. Two CellML RDF Schema are being developed for the convenience of model authors and developers of CellML processing software. The first schema will define a data model for storing elements from the Dublin Core element set, modification history information, inline documentation and specific biological metadata. The second schema will define how information about literature references should be stored in a CellML document. This schema will be an RDF serialization of the Object Management Group's Bibliographic Query Service (BQS) data model. The CellML RDF Schema will be defined and discussed in a companion metadata specification.

The table in Section 2.2.2 defines five metadata namespaces that CellML processing software is expected to recognise, and recommended prefixes to which these namespaces should be mapped. RDF elements are placed in the RDF namespace, which should be mapped to the prefix rdf. Dublin Core elements and Dublin Core qualifier attributes are placed in the appropriate namespaces, which should be mapped to the prefixes dc and dcq, respectively. CellML metadata elements and BQS citation elements each have their own namespace, mapped to prefixes of cmeta and bqs, respectively.

CellML processing software is free to ignore any and all metadata. However, it is hoped that software will at least display metadata. Model authors are free to develop their own RDF schema for metadata, or to store metadata in another format by using the CellML extension mechanism described in Section 2.2.3. However, doing so decreases the likelihood that CellML processing software will be able to do anything useful with the metadata in the model.

Metadata is defined within an <RDF> element in the RDF namespace, as shown in Figure 18. The recommended practice is to define the RDF namespace and any namespaces used by the enclosed metadata on the RDF element, even if these namespaces are already defined on the <model> element. This increases the re-usability of the RDF block. Furthermore, RDF processing software that does not recognise the CellML namespace can still parse a CellML document, extract the RDF blocks, and perhaps provide useful functionality with the information described in the RDF.

The <rdf:RDF> element contains an <rdf:Description> element, which defines an about attribute. The value of the about attribute must be a valid Uniform Resource Identifier (URI). A URI that points to a resource in the current document consists of a hash (#) followed by the value of that resource's id attribute.

Metadata is associated with a CellML document by assigning the about attribute an empty value (""). Any CellML element that has associated metadata must define an id attribute in the CellML metadata namespace (defined in Section 2.2.2). This attribute is of type ID, as defined in the XML specification. Its value must be unique across the CellML document, but need not have any meaning. Metadata is associated with a CellML element by assigning the about attribute on the <rdf:Description> element a value equal to the value of the cmeta:id attribute on the CellML element.

An RDF block should be stored in the element about which it contains metadata. This makes the element more re-useable. Elements in the MathML namespace are an exception to this recommendation. The MathML content of a <component> element might be extracted for use in a general MathML processor, which might not be able to handle RDF content. Therefore, metadata on MathML elements should be placed in the containing <component> element. If the RDF block contains metadata about the CellML document, it should be included in the root element of the document. Note that simply putting the RDF block inside an element is not sufficient to indicate that the metadata in the block refers to that element. The about attribute on the <rdf:Description> element must be used to indicate about which resource the RDF block contains metadata.

8.3  Examples

Figure 18 demonstrates the use of metadata in CellML. Three RDF blocks are shown: one that provides metadata about the CellML document, one that provides metadata about the model, and one that provides metadata about a component contained in the model. Only the RDF framework elements are shown. The actual metadata is not shown here. Examples in the companion CellML metadata specification will demonstrate how to use the recommended metadata elements.

<model
    name="example_metadata_model"
    cmeta:id="model01"
    xmlns="http://www.cellml.org/2001/03/cellml"
    xmlns:cellml="http://www.cellml.org/2001/03/cellml"
    xmlns:cmeta="http://www.cellml.org/2001/03/metadata">

  <!-- This metadata block is about the CellML document -->
  <rdf:RDF
      xmlns:cmeta="http://www.cellml.org/2001/03/metadata"
      xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#">
    <rdf:Description about="">
      <!-- Some metadata content, such as a last-modified date -->
    </rdf:Description>
  </rdf:RDF>

  <!-- This metadata block is about the CellML model -->
  <rdf:RDF
      xmlns:cmeta="http://www.cellml.org/2001/03/metadata"
      xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#">
    <rdf:Description about="#model01">
      <!--
       Some metadata content, such as a species for which
       the model is relevant.
      -->
    </rdf:Description>
  </rdf:RDF>    

  <component name="membrane" cmeta:id="comp01">

    <!-- This metadata block is about the membrane component -->
    <rdf:RDF
        xmlns:cmeta="http://www.cellml.org/2001/03/metadata"
        xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#">
      <rdf:Description about="#comp01">
        <!--
         Some metadata content, such as a annotation describing
         limitations of this representation of the membrane
        -->
      </rdf:Description>
    </rdf:RDF>
  
  </component>
  
</model>

Figure 18 An example of the use of metadata in a CellML document.

The first RDF block provides metadata about the CellML document. This is indicated by the empty value of the about attribute on the <rdf:Description> element. The second RDF block has a value of "#model01" for the about attribute on the <rdf:Description> element. This indicates that this metadata provides information about the model that is delimited by the <model> element with an cmeta:id attribute with a value of "model01". The final RDF block provides metadata about the membrane component. This is indicated by assigning a value of "#comp01" to the about attribute on the <rdf:Description> element.

Note that all three RDF blocks declare the RDF and CellML metadata namespaces. This makes the RDF blocks portable: the information needed to interpret the RDF will be preserved even if the blocks are extracted from the CellML document.

8.4  Rules for CellML Documents

8.4.1  The <rdf:RDF> element

1. Allowed use of the <rdf:RDF> element
   • Any CellML element may contain any number of <rdf:RDF> elements. [ Metadata may appear on any CellML element, and may be split across multiple <rdf:RDF> elements. The recommended practice is to enclose all metadata about a particular element in a single <rdf:RDF> element. In this and subsequent rules, the use of the rdf prefix indicates that elements and attributes are in the RDF namespace. ]
   • The content of an <rdf:RDF> element must conform to the Resource Description Framework (RDF) Model and Syntax Specification recommendation from the W3C. [ Avoid the abbreviated syntax defined in the recommendation to ensure maximum portability of the metadata. ]

8.4.2  The <rdf:Description> element

1. Allowed use of the <rdf:Description> element
   • The content of an <rdf:Description> element must conform to the Resource Description Framework (RDF) Model and Syntax Specification recommendation from the W3C. [ The recommended practice is for contained elements to adhere to an RDF schema, and to use the CellML metadata schema wherever possible. ]
2. Allowed values of the about attribute
   • The about attribute on an <rdf:Description> element must either be empty or have a value equal to a valid URI that points to an element in the current document (i.e., is equal to the value of a cmeta:id attribute on an element in the current document preceded by a hash (#)). [ An <rdf:Description> element with an empty about attribute contains information about the CellML document. An <rdf:Description> element with an about attribute that references a cmeta:id attribute value contains information about the element in the current document identified by the cmeta:id attribute. ]

8.4.3  Proper use of the cmeta:id attribute

• The cmeta:id attribute may appear on any element in a CellML document. [ In this and subsequent rules, the cmeta prefix places elements and attributes in the CellML metadata namespace. ]
• The value of the cmeta:id attribute must be unique across the CellML document.
• A cmeta:id attribute must be defined on any element in the CellML or MathML namespaces for which RDF metadata is defined.

8.5  Rules for Processor Behaviour

8.5.1  Metadata is optional

All metadata is optional. A model without any metadata is a valid CellML model. However, we strongly recommend that the modeller provide as much metadata as possible, particularly his/her name and contact information and a reference for a paper that describes the development of the model.

8.5.2  Associating metadata with resources

Software must associate the metadata contained within an RDF block with a CellML document, a CellML model, or a specific element within the CellML model according to the following rules:

• If the about attribute on an <rdf:Description> is empty, then the metadata contained within the <rdf:Description> element refers to the entire CellML document.
• If the about attribute on an <rdf:Description> points to a <model> element, then the metadata contained within the <rdf:Description> element is associated with the referenced model.
• If the about attribute on an <rdf:Description> points to any other element within the current document, then the metadata contained within the <rdf:Description> element is associated with the referenced element.

8.5.3  General meaning of metadata

Metadata may refer to the CellML document, the CellML model, or a specific element within the CellML model. The following list documents the intended meaning of metadata on each of these resources. More detailed information can be found in the companion CellML metadata specification.

• Metadata that refers to the CellML document provides information relevant to the document as a whole, independent from the use of the document to specify a model. Examples of metadata that might appear on a CellML document are last modified date (date on which the document was last edited) and publisher (person or organization distributing the document).
• Metadata that refers to the CellML model provides information relevant to the model as a whole. For instance, the model author is the person who created the complete model, even if some of the components were taken from a shared database and have different authors.
• Metadata that refers to a specific CellML element provides information about that element only. It does not provide information about elements that are contained in the referenced element.