CellML 1.1 Specification
This Version:
http://www.cellml.org/specifications/cellml_1.1
Latest Version:
http://www.cellml.org/specifications/cellml_1.1
Previous Versions:
http://www.cellml.org/specifications/cellml_1.0
Authors:
Autumn Cuellar (Bioengineering Institute, University of Auckland)
Poul Nielsen (Bioengineering Institute, University of Auckland)
Matt Halstead (Bioengineering Institute, University of Auckland)
David Bullivant (Bioengineering Institute, University of Auckland)
David Nickerson (Bioengineering Institute, University of Auckland)
Warren Hedley
Melanie Nelson
Catherine Lloyd (Bioengineering Institute, University of Auckland)
Abstract
This document specifies CellML 1.1, an XML-based language for describing and exchanging models of cellular and subcellular processes. MathML embedded in CellML documents is used to define the underlying mathematics of models. Models consist of a network of re-usable components, each with variables and equations manipulating those variables. Models may import other models to create systems of increasing complexity. Metadata may be embedded in CellML documents using RDF.
Status of this document
The 6 November 2002 version of the CellML 1.1 specification has been reviewed
and endorsed by all of the authors of and contributors to the document. As of
28 February 2006, the syntax and semantics of all of the elements in the CellML
1.1 namespace are frozen.
The authors invite feedback from the public. Readers are encouraged to subscribe
and send comments and questions to the cellml-discussion@cellml.org mailing
list.
The latest version of the CellML specification is always available at the
following URI:
http://www.cellml.org/specifications
The list of errata associated with this document is available at the following
URI:
http://www.cellml.org/specifications/cellml_1.1/errata
Contents
- 1 Introduction
- 2 Fundamentals
- 3 Model Structure
- 4 Mathematics
- 5 Units
- 6 Grouping
- 7 Reactions
- 8 Metadata Framework
- 9 Importing Models
- 10 Using The CellML 1.1 DTD
- 11 Scripting Functionality in CellML
- 12 Advanced Units Functionality
- 13 Changes
1 Introduction
1.1 Introduction to CellML
This document specifies CellML 1.1, an XML-based language for describing and exchanging models of cellular and subcellular processes. CellML is being developed by scientists at the University of Auckland (in the Bioengineering Institute) and at Physiome Sciences, Inc. The development of CellML is guided by an advisory board drawn from many different areas of biological modelling (see the project team page on the CellML website for more information). CellML is being developed as an open standard, and all interested parties are encouraged to send feedback to info@cellml.org, or to the cellml-discussion mailing list.
1.1.1 Purpose and scope of CellML
CellML is intended to support the definition of models of cellular and subcellular processes. CellML facilitates the reuse of models and parts of models by using a component-based architecture. Models are split into logical sub-parts called components that are connected together to form a model.
CellML separates the specification of the underlying mathematics of a model from the implementation of the model's solution. This makes a model independent of a particular operating system or programming language and allows modellers to easily integrate parts of other peoples' models into their own models. CellML also allows the generation of equations for publishing from the same definition upon which the solution method is based, removing inconsistencies between the model and associated results in academic papers, and allowing others to reliably reproduce these results.
The scope of the CellML language is specifically limited to the definition of model structure. All other types of information that modellers need or want to include in a model document are incorporated using other languages. For instance, mathematics is included in CellML documents using Mathematical Markup Language (MathML). Metadata may be included using the Resource Description Framework.
1.1.2 What is XML?
The CellML language is defined in terms of a meta-language called eXtensible Markup Language (XML). XML is a standard published by the World Wide Web Consortium, the organisation responsible for defining many internet-related standards, including HTML. XML is essentially a means of adding structure to text documents, allowing machines to unambiguously associate text or binary data with a particular component in a document's data model.
XML is an appropriate medium for CellML because it is both human and machine readable. A model author can create a CellML document with a text editor or with CellML authoring software. XML is a well-defined and widely used specification. Many free software utilities and libraries for the processing of XML already exist, simplifying the development of CellML processing software. XML has also been designed to be usable over the internet, making CellML suitable for the interchange of models between software and databases at different locations.
A quick introduction to XML is available in the examples section of the CellML website.
1.1.3 Terminology
A model is a representation of the rules that govern the behaviour of a system. The terms in the following list provide two useful model classifications.
qualitative model
A model that defines the relationships between objects in the system, without defining any mathematics that represent the behaviour of those objects.
quantitative model
A model that defines the relationships between objects in the system, including the mathematics that represents the behaviour of those objects.
The terms defined in the following list are used in specifying the conformance of CellML documents and processing software to this specification.
may
Conforming CellML documents are permitted but not required to adhere to the limitation described. Conforming CellML software is permitted but not required to behave as described.
must
Conforming CellML documents must adhere to the limitation described. Conforming CellML software must behave as described.
for interoperability
A non-binding recommendation included to increase the chances that CellML documents will be processed in a consistent manner by different applications.
error
A violation of the rules of this specification; results are undefined. Conforming CellML software may detect and report an error and may recover from it. The recommended best practice is for software to make information about errors available to the user.
valid CellML document
A document that conforms to all of the rules in this specification.
valid CellML subset document
A valid CellML document that only uses MathML elements from the CellML subset defined in Section 4.2.3.
CellML conformant software
CellML processing software that will interpret any valid CellML subset document according to the language semantics and processor rules defined in this specification.
fully MathML capable software
Software that can correctly interpret the full set of MathML content markup elements.
1.2 Structure of the CellML Specification
The CellML specification is divided into several sections, each of which discusses a particular aspect of CellML:
- Section 1 — Introduction — This section introduces CellML, XML, the terminology used throughout the specification, and the structure of the specification.
- Section 2 — Fundamentals — This section explains concepts used in all other sections of the specification, such as the definition of a valid CellML identifier and the use of XML namespaces in CellML.
- Section 3 — Model Structure — This section describes how models are organised in CellML. It includes an explanation of the use of a network of components to define a model and a discussion of variables in CellML.
- Section 4 — Mathematics — This section describes how mathematical expressions are defined in CellML documents using MathML and defines the CellML subset of MathML elements.
- Section 5 — Units — This section explains the requirements for units in CellML and describes how a modeller can define arbitrary sets of units.
- Section 6 — Grouping — This section explains how a model can be organised into logical encapsulation and geometric containment hierarchies by grouping components.
- Section 7 — Reactions — This section introduces CellML syntax that allows the modeller to classify the involvement of the participants in the chemical expressions that make up reaction/pathway models.
- Section 8 — Metadata Framework — This section describes how RDF is used in CellML documents to define metadata and associate it with models, model components, and other CellML elements.
- Section 9 — Importing Models — This section explains how a model may be built on existing models. The import feature also allows a modeller to create an incomplete model, with the expectation that the necessary components and connections may be included in the future.
- Appendices — The appendices cover advanced and technical topics including the CellML DTD, recommendations for adding scripts to CellML documents, and units processing algorithms.
A valid CellML model can be created using nothing beyond the material covered in the fundamentals, model structure, mathematics, and units sections of the specification. The concepts in the remaining sections of the specification allow modellers to build more meaningful models.
Each section of the specification is further divided into five subsections:
- Introduction — This subsection explains the purpose of the elements covered in the current section.
- Basic Structure — This subsection describes the new elements and attributes introduced in the current section of the specification and how they are combined.
- Examples — This subsection provides one or two basic examples of the correct use of the elements and attributes introduced in the current section of the specification. More extensive examples can be found in the repository of the CellML website.
- Rules for CellML Documents — This subsection provides formal rules for the use of the elements and attributes introduced in the current section to create valid CellML documents. These rules are specified as bulleted lists. Each rule may have an associated explanation, which appears directly after the rule in square brackets ([]).
- Rules for Processor Behaviour — This subsection provides some rules for correct CellML processor behaviour with regards to the elements and attributes introduced in the current section.
Throughout the CellML specification, all XML elements and attributes that occur in the text are in the CellML namespace unless explicitly stated otherwise.
2 Fundamentals
2.1 Introduction
This section of the CellML specification introduces some concepts that are used throughout the entire language and defines rules that apply to all or many of the other parts of the specification. These include the definition of names and use of namespaces in CellML.
2.2 Basic Structure
2.2.1 Definition of a valid CellML identifier
The most common use of a CellML identifier is the name attribute required on many basic elements in CellML. The value of this attribute can be used to reference that element from elsewhere in the model definition or from another model definition altogether. An object's name can generally be thought of as a unique identifier for that object. Although the XML specification defines a mechanism for specifying that the value of an attribute is unique across an entire document (with the ID attribute type), this functionality is not used in CellML 1.1 because an object's name need only be unique across its own class of objects.
The generation of computer code for running simulations is one of the target applications for CellML. The value of an object's name attribute is intended to be a suitable name for the same object when it is represented in computer code. For this reason CellML identifiers must consist of only alphanumeric characters and the underscore character ("_"), and are subject to some additional constraints outlined below. These names will generally not be the most effective way of identifying the object to humans working with CellML models as it is not possible to include whitespace or formatting. More human readable names can be defined and associated with CellML objects using the metadata functionality introduced in Section 8.
The XML specification is based on the Unicode standard, which defines a scheme for 16 bit character encoding. Thus it is possible to include, for instance, Japanese characters in a valid XML document. In the interests of making the code generation process as convenient as possible for those using mainstream programming languages, CellML identifiers are subject to the following constraints:
- An identifier must consist only of alphanumeric characters from the US-ASCII character set and underscore characters,
- An identifier must contain at least one letter, and
- An identifier must not begin with a digit.
Convenient code generation is also the reason why colons, periods, and hyphens may not appear in CellML identifiers. CellML identifiers are case sensitive: a variable with an identifier of ABC is different from a variable with an identifier of abc.
2.2.2 Namespaces in CellML
Namespaces in XML is a companion specification to the XML 1.0 specification. XML namespaces add a second level of naming to elements and attributes, allowing processing software to distinguish between elements and attributes from different languages. A namespace is identified by a Uniform Resource Identifier (URI), which has the feature of being unique. The value of a namespace URI need have nothing to do with the XML document that uses it. However, it typically points to a document that defines the rules for the language. The URI may be mapped to a prefix, which may then be used in front of element and attribute names, separated by a colon. If not mapped to a prefix, the URI sets the default namespace for the current element and all of its children.
The CellML 1.1 specification defines a small number of elements and attributes and a namespace with which they must be associated. Putting CellML elements and attributes in the CellML namespace allows them to be distinguished from elements and attributes from other vocabularies with which CellML syntax might be combined in a CellML document. For instance, CellML makes use of the MathML vocabulary for the definition of equations, and all MathML elements must be placed in the MathML namespace in order for CellML processing software to recognise those elements. The use of namespaces also allows processing software to distinguish elements and attributes from different versions of the CellML specification. Applications that store their own proprietary data within a CellML document must define their own namespaces and associate their own elements and attributes with those namespaces, as discussed in Section 2.2.3.
This specification is primarily concerned with the rules and semantics that relate to the elements and attributes in the CellML namespace, which are used in the definition of model structure. It is an error if documents contain elements and attributes in the CellML namespace that are not defined in this specification. This specification also defines how elements and attributes in the MathML, XLink, RDF and CellML Metadata namespaces can be combined with elements and attributes in the CellML namespace, and how processing software should deal with content in those namespaces. MathML is particularly important to CellML because content in this namespace is considered as fundamental as content in the CellML namespace. The CellML import feature makes use of the W3C hyperlink standard, XLink, to refer to other models. Metadata is defined using elements in the RDF namespace and linked to CellML elements using an id attribute in the CellML Metadata namespace as described in Section 8. Any CellML element may contain elements and attributes in other namespaces, which CellML processing software is free to ignore.
Table 1 lists the names, URIs and recommended prefixes of the namespaces referenced in this specification. For interoperability, the root element of any CellML document should set the default namespace and map the cellml prefix to the CellML 1.1 namespace URI. The latter simplifies the association of elements and attributes with the CellML namespace in regions of the document where the default namespace is not the CellML namespace. For instance, the MathML elements used to define equations are typically placed inside a <math> element that changes the default namespace to the MathML namespace. A cellml:units attribute in the CellML namespace can then be added to each of MathML's <cn> elements without having to redeclare the CellML namespace every time it is used.
| Namespace Name | Namespace URI | Recommended Prefix |
|---|---|---|
| CellML | "http://www.cellml.org/cellml/1.1#" |
cellml |
| CellML Metadata | "http://www.cellml.org/metadata/1.0#" |
cmeta |
| MathML | "http://www.w3.org/1998/Math/MathML" |
mathml |
| XLink | "http://www.w3.org/1999/xlink" |
xlink |
| RDF | "http://www.w3.org/1999/02/22-rdf-syntax-ns#" |
rdf |
Table 1 The names, URIs and recommended prefixes of the namespaces referenced in this specification. See text for more details.
2.2.3 Extending CellML documents
Any namespace with a URI not defined in Table 1 is an extension namespace. Any element in an extension namespace is an extension element. Any attribute in an extension namespace is an extension attribute. Model authors and CellML processing software may store information not covered by the CellML specification in a CellML document by defining their own extension elements and extension attributes. When authors and implementors define extension namespaces, it is recommended that they use URIs under their jurisdiction. Extension elements and extension attributes may appear anywhere in a CellML document as long as the result is well-formed XML.
For interoperability CellML processing software should respect the extension elements and attributes of other applications. If a model is created in application A, which adds its own extension elements, and is subsequently edited in application B, then application B should attempt to include application A's extension elements in its output, even if these extension elements are now invalid. Applications will need to validate their own extension data if a CellML document is read in from a non-trusted location.
The namespace extension mechanism provides a convenient way to associate a small amount of application-specific information with a model defined in CellML. However, it is recommended that applications needing to store large amounts of information, such as rendering or simulation information, do so in a separate document. This will make CellML documents easier to exchange and will prevent the loss of application-specific information if the model is passed through applications unaware of the extensions.
2.3 Examples
Figure 1 contains some example CellML elements, each of which defines a name attribute. The values of the name attribute on the first three elements are valid CellML identifiers. The values of the name attribute on the last three elements are invalid identifiers.
Figure 1 XML elements defining name attributes. Valid and invalid CellML identifiers are shown, as noted in the comments.
Figure 2 contains portions of a typical CellML document that demonstrate the recommended use of namespaces. The root element sets the default namespace to the CellML namespace URI and explicitly maps the CellML namespace URI to the cellml prefix. The <math> element that encloses a set of equations inside a component element resets the default namespace to the MathML namespace. The units attribute on the <cn> element (which is in the MathML namespace) is placed in the CellML namespace by using the previously-defined cellml prefix.
Figure 2 A CellML fragment demonstrating the recommended use of namespaces in a CellML document. This fragment is taken from the simple electrophysiological model example on the CellML website.
Figure 3 demonstrates how software can embed its own information inside a valid CellML document using XML namespaces. The <model> element sets the default namespace to the CellML namespace, and maps the app prefix to an extension namespace (i.e., one not defined in Table 1). The app prefix is then used to define an <app:component_rendering_information> element and two attributes on a <component> element.
Figure 3 A CellML document demonstrating the use of XML namespaces to embed application specific data inside a CellML document. The extension namespace URI was invented for demonstration purposes only.
2.4 Rules for CellML Documents
2.4.1 Valid CellML identifiers
- A valid CellML identifier must consist of only letters, digits and underscores, must contain at least one letter, and must not begin with a digit. This can be written using Extended Backus-Naur Form (EBNF) notation as follows:
letter ::= 'a'...'z','A'...'Z'
[ The variant of EBNF used above is defined in Section 6 of the XML 1.0 Recommendation. ]
digit ::= '0'...'9'
identifier ::= ('_')* ( letter ) ( letter | '_' | digit )*
2.4.2 Proper use of the CellML namespace
- A document must not contain elements or attributes in the CellML namespace that are not defined in this specification. [ Documents containing unknown elements or attributes in the CellML namespace are not valid CellML documents. Rules regarding the use of elements in the other namespaces defined in Table 1 are given in the appropriate sections. Note that attributes without an explicit prefix declaration are assumed to be in the same namespace as their parent element. ]
2.4.3 Extension namespaces
- Although not explicitly stated throughout this specification, a document author may add extension elements and extension attributes to any CellML element in a CellML document without affecting the validity of the document. [ Note that attributes without an explicit prefix declaration are assumed to be in the same namespace as their parent element. ]
- For interoperability, elements in the CellML namespace should not be defined inside extension elements. [ Specifically, applications should not define important model structure, mathematics or metadata information within extension elements, which other applications are free to ignore. ]
- For interoperability, attributes in the CellML namespace should not be defined on extension elements.
2.4.4 Text nodes within CellML elements
- Any characters that occur immediately within elements in the CellML namespace must be either space (
#x20) characters, carriage returns (#xA), line feeds (#xD), or tabs (#x9). [ All of the elements in the CellML 1.1 namespace contain no text content. The characters listed above correspond to the definition of whitespace given in Section 2.3 of the XML Recommendation. Text content may still be included in extension elements inside CellML elements. ]
2.5 Rules for Processor Behaviour
2.5.1 Treatment of CellML identifiers
- CellML processing software must handle identifiers in a case-sensitive manner. [ Two CellML elements of the same type may be defined with identifiers of
Aanda. Processing software is expected to match the identifiers in a case-sensitive manner when those elements are referenced at other places in the document. ]
2.5.2 Treatment of attribute namespaces
- CellML processing software must treat attributes without an explicit namespace declaration as if they were in the same namespace as their parent element.
2.5.3 Treatment of extension namespaces
- CellML processing software may ignore extension elements and extension attributes. [ If the namespace is unrecognised, then software should probably alert the user to its presence. Polite software should attempt to store non-CellML data so that it can write it out again when it exports the document. Software should validate its own non-CellML data carefully when reading documents from a non-trusted location. ]
- CellML processing software may ignore the attributes and content of extension elements.
3 Model Structure
3.1 Introduction
Any model can be described as a network of connections between self-contained components. A component is a functional unit that may correspond to a physical compartment, event, or species or may be just a convenient modelling abstraction. A component contains variables and mathematical relationships that manipulate those variables. Connections exchange information between components. A connection contains mappings between variables in two components, allowing the value of a variable in one component to be passed to a variable in the other component.
3.2 Basic Structure
3.2.1 Definition of a model
A model is declared in CellML with a <model> element. This is the usual root element for a CellML document. The recommended best practice for specifying namespaces in a CellML document is described in Section 2.2.2.
The <model> element has a name attribute that allows the model to be unambiguously referenced. A <model> element may contain any number of the elements in the following list in any order. However, the recommended best practice is for elements placed within the <model> element to appear in the order given in the following list. This allows people to quickly find certain kinds of information within a CellML document.
-
<import>— A modeller may import parts of another valid CellML model, as described in Section 9. -
<units>— A modeller can declare a set of units to use in the model, as described in Section 5. -
<component>— Components are the smallest functional units in a model. Each component may contain variables that represent the key properties of the component and/or mathematics that describe the behaviour of the portion of the system represented by that component. -
<group>— Groups allow the modeller to define logical and physical relationships between components. Groups are defined using the<group>element, as discussed in Section 6. -
<connection>— Connections are used to connect components to each other and to map variables in one component to variables in another. Connections are defined using the<connection>element, as discussed in Section 3.2.4.
The <model> element (and indeed any of the elements in a CellML document) may define metadata to provide context for that object. This metadata might include documentation, citations from literature, or a modification history for the current CellML object. Adding metadata to a CellML document is discussed in detail in Section 8.
3.2.2 Definition of components
Constructing a model from multiple components encourages the reuse of components. For instance, an electrophysiological model of a cell might be organised into components that represent various ion channels. All of the mathematics that describe the behaviour of the L-type calcium channel would be defined in a single component representing this particular ion channel. If a modeller wished to reuse the portion of the model representing the L-type calcium channel in another model, he or she would only need to import this component into a second model. See Section 9 for more information on the import feature.
A <component> element is used to declare a CellML component. It must only be used inside a <model> element or an <import> element.
A CellML <model> may contain any number of <component> elements. Each <component> must have a name attribute, the value of which is a unique identifier for the component amongst all other components within the current model. The value of the name attribute is used to reference the component in other parts of the model, such as in connections and groups. If a component is being declared in an <import> element, the <component> element must also have a component_ref attribute. The component_ref attribute is explained in Section 9.
A <component> may contain any of the elements in the following list in any order. Again, recommended best practice is for elements placed within the <component> element to appear in the order given in the following list.
-
<units>— A modeller can define a set of units to use within the component, as described in Section 5. -
<variable>— A component may contain any number of<variable>elements, which define variables that may be mathematically related in the equation blocks contained in the component. Variables are discussed in Section 3.2.3. -
<reaction>— A component may contain<reaction>elements, which are used to provide chemical and biochemical context for the equations describing a reaction. It is recommended that only one<reaction>element appear in any<component>element. The definition of reaction information is described in Section 7. -
<mathml:math>— A component may contain a set of mathematical relationships between the variables declared in this component. These equations are marked up using MathML, as discussed in Section 4. Themathmlprefix is used to indicate that the<math>element is in the MathML namespace.
A <component> element is also a sensible place to define metadata, using the syntax presented in Section 8.
The definitions of two <component> elements are included in the example described in Section 3.3.
3.2.3 Definition of variables
Models are usually developed to investigate the behaviour of a number of variables that have biological significance. Each variable in the model belongs to a single component, which may contain equations that modify the value of that variable. The value of a variable may be passed through connections into other components. The variable must also be declared in these components, which can then use the value of the variable in their own equations but must not modify it.
The <variable> element is used to declare a CellML variable. It can only be used inside a <component> element. Variables must define a name attribute, the value of which must be unique across all variables in the current component. The name of a variable is used when referencing variables inside connections (see Section 3.2.4) and reactions (see Section 7). All variables must also define a units attribute. The value of this attribute must correspond to one of the keywords in the CellML units dictionary or the value of the name attribute of a <units> element defined within the current component or model, as described in Section 5.
A <variable> element may also have the following attributes:
-
initial_value— This attribute provides a convenient means for specifying the value of a scalar real variable when all independent variables in the model have a value of 0.0. Independent variables are those whose values do not depend on others. -
public_interface— This attribute specifies the interface exposed to components in the parent and sibling sets (see below). The public interface must have a value of"in","out", or"none". The absence of apublic_interfaceattribute implies a default value of"none". -
private_interface— This attribute specifies the interface exposed to components in the encapsulated set (see below). The private interface must have a value of"in","out", or"none". The absence of aprivate_interfaceattribute implies a default value of"none".
The name of the initial_value attribute is derived from the fact that, in a model with only one independent variable, this would generally correspond to time, and so the value of the initial_value attribute sets the starting condition for a simulation which progressed from time equals 0.0. The value of the initial_value attribute may be a real number or a variable. A modeller may wish to store the initial and boundary conditions in a separate file that is imported by the current model. See Section 9 for more information on CellML's import feature.
Whether or not a component may obtain the value of a variable in another component depends on the public_interface and private_interface attributes on the variable declaration and on the place of the two components in the encapsulation hierarchy. Encapsulation allows the modeller to hide a complex network of components from the rest of the model and provides a single component as an interface to the hidden network. Encapsulation effectively divides the network into layers, where connections between the layers must only be made through the interface components.
The components to which any given component may connect can be divided into four distinct sets with respect to any given component (the current component). The set of all components immediately encapsulated by the current component is referred to as the encapsulated set. If the current component is encapsulated, then the encapsulating component is referred to as the parent, and the set of all other components encapsulated by the same parent is referred to as the sibling set. If the current component is not encapsulated, then it has no parent and the sibling set consists of all other components in the model that are not encapsulated. All other components, which are not available to make connections with the current component, make up the hidden set. The encapsulation hierarchy and its effects on variable mapping are described in Section 6.
When a variable is declared with either a public_interface or private_interface attribute value of "in", then the value of that variable must be imported from another component. Otherwise, a variable's value must be set and modified in the current component. The variable is then said to belong to or be owned by the current component.
Eventually, it will be possible to specify the temporal and/or spatial variation of a variable's value using FieldML. The capability to include FieldML is still under development. At the present time, all variables must have scalar real values.
3.2.4 Definition of connections
Connections provide the mechanism for mapping variables declared within one component to variables in another component, allowing information to be exchanged between the various components in the network. The mapping of variables involves the transfer of a variable's value from one component to another, a process which may involve a conversion to ensure the units match. (More information on units conversion can be found in Section 5.)
The complete set of variable mappings between any two components constitutes a connection. Only one connection may be created between any given pair of components in a model. Each connection references the two components involved in the connection, and then maps variables from each of the components together. The interface attributes of each pair of variables must be compatible — an "out" variable in one component's interface must map to an "in" variable in the other component's interface. The direction of each mapping is determined by the value of the public_interface and private_interface attributes on the two variables: the value is always passed from the variable with an interface value of "out" to the variable with an interface value of "in". The value of a variable declared with an interface value of "out" may be passed out to any number of variables in other components declared with interface values of "in". The component to which a variable belongs is found by tracing the variable back from "in" to "out" interfaces, following the model's connections.
The <connection> element is used to declare a CellML connection. It can only appear inside a <model> element.
A <connection> element must contain exactly one <map_components> element, which is used to reference the two components involved in the connection. Each <map_components> element must define component_1 and component_2 attributes, the values of which are the names of the components being referenced. The referenced components must appear as a new definition in the current <model> element or be an imported component from another model declared as a child of the <import> element.
A <connection> element must also contain one or more <map_variables> elements, which are used to reference the variables being mapped between the two components in the connection. Each <map_variables> element must define variable_1 and variable_2 attributes, the values of which are equal to the names of variables defined in the components referenced by the component_1 and component_2 attributes on the <map_components> element, respectively. It is not necessary for the variables that are to be mapped to each other to have the same name, although this will typically be the case.
The CellML example discussed in Section 3.3 demonstrates the definition of a <connection> element.
3.3 Examples
Figure 4 contains a portion of the CellML description of the Hodgkin-Huxley squid axon model published in 1952. The excerpt contains the definitions of the components corresponding to the membrane and the sodium channel, and the connection between the two components. Most of the complexity from the full model definition has been left out for conciseness and clarity. This example is only used to demonstrate the standard use of the <component>, <variable>, and <connection> elements.
Figure 4 A small portion of the CellML description of the Hodgkin-Huxley squid axon model from 1952. This excerpt contains the definition of the components corresponding to the membrane and the sodium channel, and the connection between them. Much detail has been omitted, but this example clearly demonstrates the relationship between the <component>, <variable> and <connection> elements.
The membrane component declares six variables, which are divided into three categories. The first variable is called V, and it represents the membrane voltage in the model. It has a public_interface attribute value of "out", which indicates that the variable "belongs" to this component and that its value may be obtained by other components in the model via connections. It references a units definition by the name of millivolt (this definition is not included here) and is given an initial value of -75.0 millivolts.
The subsequent four variables are time, i_Na (sodium current), i_K (potassium current) and i_L (leakage current). They are all declared with a public_interface attribute value of "in", which indicates that their values are obtained from other components via connections.
Finally, a variable C (capacitance) is declared. This <variable> element defines neither a public_interface or a private_interface attribute. Both of these attributes therefore assume the default value of "none", which means that the variable belongs to the current component and is not visible to other components in the model.
After the variable declarations, a <math> element in the MathML namespace is used to define an equation relating V to the other variables. Only the values of the variables belonging to a component may be mathematically modified in that component. The equation included in Figure 4 is the well known differential equation from the Hodgkin Huxley model:
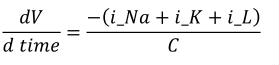 |
(1) |
The sodium_channel component declares three variables, all of which represent quantities that were also declared in the membrane component. The i_Na variable declared in this component has a public_interface attribute value of "out", indicating that the sodium current belongs to this component. The value of the sodium current is calculated in this component, although the actual math has been omitted.
Finally, a <connection> element references the membrane and sodium_channel components using a <map_components> element, and maps the V and i_Na variables in each component together, using two <map_variables> elements. The value of the variable_1 attribute on each <map_variables> element references the corresponding variable in the membrane component, since this is the component referenced by the component_1 attribute on the <map_components> element. Similarly, the values of the variable_2 attributes reference variables in the sodium_channel component.
3.4 Rules for CellML Documents
The following are the rules for using the <model>, <component>, <variable>, <connection>, <map_components>, and <map_variables> elements.
3.4.1 The <model> element
- Allowed use of the
<model>element- A
<model>element must contain only the following elements, which may appear in any order:-
<import>,<units>,<component>,<group>, and<connection>elements in the CellML namespace, <RDF>elements in the RDF namespace.
-
- Each
<model>element must define anameattribute.
- A
- Allowed values of the
nameattribute- The value of the
nameattribute must be a valid CellML identifier as discussed in Section 2.2.1.
- The value of the
3.4.2 The <component> element
- Allowed use of the
<component>element- A
<component>element appearing as the child of a<model>element must contain only the following elements, which may appear in any order:<units>,<variable>and<reaction>elements in the CellML namespace,-
<math>elements in the MathML namespace, <RDF>elements in the RDF namespace.
<component>element must not appear inside another<component>element. Such nesting could be intended to indicate a logical encapsulation relationship, a geometric containment relationship, or some other relationship between the two components. There is no reason to assume that the nesting hierarchy produced for one type of relationship would be consistent with the hierarchy produced for other types of relationships. Therefore, CellML defines these relationships using the<group>element, rather than nesting of<component>elements. ] - A
<component>element appearing as the child of an<import>element must contain only the following elements, which may appear in any order:<RDF>elements in the RDF namespace.
- Each
<component>element must define anameattribute. - Each
<component>element appearing as the child of an<import>element must additionally define acomponent_refattribute.
- A
- Allowed values of the
nameattribute- The value of the
nameattribute must be a valid CellML identifier as discussed in Section 2.2.1. - The value of the
nameattribute must be unique across all<component>elements contained in the parent<model>element.
- The value of the
- Allowed values of the
component_refattribute- The value of the
component_refattribute must equal the value of the name attribute of a component defined in the model at the URI given on the parent<import>element. [ Thecomponent_refattribute is a general construct for pointing to another component. In future versions of CellML, thecomponent_refattribute may have a wider application, but for this version, the only context in which it is valid is on the<component>element within an<import>element. ]
- The value of the
- Proper use of the
component_refattribute- A
component_refattribute must not be defined on a<component>element appearing as a child of a<model>element. [ Acomponent_refattribute would have no meaning on a component definition not appearing inside an<import>element. ]
- A
3.4.3 The <variable> element
- Allowed use of the
<variable>element- A
<variable>element must contain only the following elements:<RDF>elements in the RDF namespace.
- Each
<variable>element must define anameattribute and aunitsattribute. It may also definepublic_interface,private_interface, andinitial_valueattributes.
- A
- Allowed values of the
nameattribute- The value of the
nameattribute must be a valid CellML identifier as discussed in Section 2.2.1. - The value of the
nameattribute of a<variable>element must be unique across all<variable>elements contained in the same<component>element. [ Two variables in the same component must not have the same name. However, two variables in different components may have the same name, and a variable may have the same name as its parent component. ]
- The value of the
- Allowed values of the
unitsattribute- The value of the
unitsattribute must either be one of the keywords defined in the standard dictionary or the value of thenameattribute on a<units>element defined in the current component or model. [ The dictionary and the units element are described in Section 5. ]
- The value of the
- Allowed values of the
public_interfaceattribute- If present, the value of the
public_interfaceattribute must be"in","out", or"none". - If not present, its value defaults to
"none".
- If present, the value of the
- Allowed values of the
private_interfaceattribute- If present, the value of the
private_interfaceattribute must be"in","out", or"none". - If not present, its value defaults to
"none".
- If present, the value of the
- Proper use of the
public_interfaceandprivate_interfaceattributes- A
<variable>element must not define bothpublic_interfaceandprivate_interfaceattributes with values equal to"in". [ A variable's value must only be obtained via one mapping. ]
- A
- Allowed values of the
initial_valueattribute- If present, the value of the
initial_valueattribute may be a real number or the value of thenameattribute of a<variable>element declared in the current component. - The absence of an
initial_valueattribute implies nothing. [ The absence of this attribute would usually mean either that the variable does not need an initial value or that this value will be supplied in a parameter file or by the user at the time simulations using the model are run. ]
- If present, the value of the
- Proper use of the
initial_valueattribute- An
initial_valueattribute must not be defined on a<variable>element with apublic_interfaceorprivate_interfaceattribute with a value of"in". [ These variables receive their value from variables belonging to another component. ]
- An
3.4.4 The <connection> element
- Allowed use of the
<connection>element- A
<connection>element must contain only the following elements, which may appear in any order:<map_components>and<map_variables>elements in the CellML namespace,<RDF>elements in the RDF namespace.
- Each
<connection>element must contain exactly one<map_components>element. - Each
<connection>element must contain at least one<map_variables>element. [ It does not make sense to define a connection that does not map variables together. This rule prevents software from using empty connections to imply information not defined in this specification. ]
- A
3.4.5 The <map_components> element
- Allowed use of the
<map_components>element- A
<map_components>element must contain only the following elements:<RDF>elements in the RDF namespace.
- Each
<map_components>element must define acomponent_1attribute and acomponent_2attribute.
- A
- Allowed values of the
component_1attribute- The value of the
component_1attribute must equal the value of thenameattribute of a<component>element contained within the current<model>element.
- The value of the
- Allowed values of the
component_2attribute- The value of the
component_2attribute must equal the value of thenameattribute of a<component>element contained within the current<model>element.
- The value of the
- Proper use of the
component_1andcomponent_2attributes- The
component_1andcomponent_2attributes on a single<map_components>element must not have the same value. [ A connection must link two different components. ] - Each
<map_components>element contained within<connection>elements that are contained within a given<model>element must define a unique pair ofcomponent_1andcomponent_2attribute values. [ There can only be one connection between any two components in a network. This prevents setting up inconsistent, circular, or duplicate variable mappings between any two components in the network. However, it does not prevent a model author from creating inconsistent mathematical relationships between the variables. ]
- The
3.4.6 The <map_variables> element
- Allowed use of the
<map_variables>element- A
<map_variables>element must contain only the following elements:<RDF>elements in the RDF namespace.
- Each
<map_variables>element must define avariable_1attribute and avariable_2attribute.
- A
- Allowed values of the
variable_1attribute- The value of the
variable_1attribute must equal the value of thenameattribute of a<variable>element contained in the<component>element referenced by thecomponent_1attribute on the<map_components>element within the current<connection>element.
- The value of the
- Allowed values of the
variable_2attribute- The value of the
variable_2attribute must equal the value of thenameattribute of a<variable>element contained in the<component>element referenced by thecomponent_2attribute on the<map_components>element within the current<connection>element.
- The value of the
- Proper use of the
<map_variables>element to map variables to each other[ The rules for mapping a variable to other variables depend on the encapsulation hierarchy of the component that owns the variable. This hierarchy divides the rest of the components in the model into parent, sibling, encapsulated, and hidden sets, as described in Section 3.2.3. The
public_interfaceattribute defines the availability of a variable to the parent component and components in the sibling set. Theprivate_interfaceattribute defines the availability of a variable to components in the encapsulated set. Variables are not available to components in the hidden set. ]- Variables with a
public_interfaceorprivate_interfaceattribute value of"in"must be mapped to variables with apublic_interfaceorprivate_interfaceattribute value of"out". - A variable with either a
private_interfaceorpublic_interfaceattribute value of"in"must be mapped to no more than one other variable in the model. [ Note that a similar restriction does not apply to variables with interface values of"out". An output variable can be mapped to multiple input variables in various components in the current model. ] - A variable with a
public_interfaceattribute value of"in"must be mapped to a single variable owned by a component in the sibling set, provided the target variable has apublic_interfaceattribute value of"out", or to a single variable owned by the parent component, provided the target variable has aprivate_interfaceattribute value of"out". - A variable with a
public_interfaceattribute value of"out"may be mapped to variables owned by components in the sibling set, provided the target variables havepublic_interfaceattribute values of"in". It may also be mapped to variables owned by the parent component, provided the target variables haveprivate_interfaceattribute values of"in". - A variable with a
private_interfaceattribute value of"in"may be mapped to a single variable owned by a component in the encapsulated set, provided the target variable has apublic_interfaceattribute value of"out". - A variable with a
private_interfaceattribute value of"out"may be mapped to variables owned by components in the encapsulated set, provided the target variables havepublic_interfaceattribute values of"in".
- Variables with a
3.5 Rules for Processor Behaviour
3.5.1 Mapping of variables
For interoperability, CellML processing software should take into account the units definitions referenced by any two variables that are mapped together. If the units references are not equivalent, as defined in Appendix C.2.1, then a conversion may be required. An algorithm for performing this conversion is proposed in Appendix C.3.5.
4 Mathematics
4.1 Introduction
CellML allows modellers to unambiguously specify the underlying mathematics of a cellular model. Model components may contain mathematical expressions that manipulate the values of variables that belong to them. These expressions are also free to use (but must not modify) the values of any other variable declared in those components.
Mathematical expressions are embedded in CellML documents using Mathematical Markup Language 2.0 (MathML), an XML-based language that encodes the underlying structure of a mathematical expression. CellML uses a subset of the elements from MathML 2.0, known as the content markup element set, which includes several deprecated elements from MathML 1.0.
CellML 1.1 does not require processing software to implement support for scripting. If software chooses to do so, some recommendations on the use of scripting are given in Appendix B.
4.2 Basic Structure
4.2.1 Definition of mathematics
All mathematical expressions defined using MathML must be placed inside a <mathml:math> element. <mathml:math> elements must only be defined in <cellml:component> or <cellml:role> elements. The mathml and cellml namespace prefixes are used throughout this section to indicate that elements are in the MathML and CellML namespaces, respectively. The <cellml:role>, <cellml:variable_ref> and <cellml:reaction> elements mentioned in this section are described in detail in Section 7 of this specification.
<mathml:math> elements that occur as child elements of <cellml:component> elements can be used to define arbitrary expressions relating the variables declared in that component. A mathematical expression may make use of any variable declared within the current component by placing the variable's name within a <mathml:ci> element. Expressions must only modify the values of variables that belong to that component. Variables that belong to a component are those that are not declared with a public_interface or private_interface attribute value of "in".
<mathml:math> elements that occur as child elements of <cellml:role> elements (these are defined within <cellml:variable_ref> elements, which are in turn defined within <cellml:reaction> elements) can be used to define expressions that modify the values of specific variables in specific ways. These expressions may make use of any variable declared in the current component but must only modify the value of the variable referenced by the ancestor <cellml:variable_ref> element, subject to further limitations that are described in Section 7.2.
CellML processing software must interpret MathML elements according to the semantics defined in the MathML 2.0 Recommendation. However, CellML 1.1 does define some restrictions on, and additions to, the MathML syntax. These are covered in the subsequent sections.
4.2.2 MathML's presentation and content markup elements
The complete set of elements defined in the MathML 2.0 Recommendation is split into two principal sub-vocabularies: the presentation markup and content markup elements. The presentation markup elements describe the visual rendering of mathematical expressions and objects. The content markup elements specify the underlying meaning of a mathematical expression or object, without regard to its presentation.
CellML is used to describe the structure and mathematics of cellular models. For this reason, valid CellML documents must only contain content markup elements within a <mathml:math> element. There is one exception: model authors may associate rendering information with a particular expression by placing MathML presentation markup elements inside a <mathml:annotation-xml> element. CellML processing software may ignore the contents of <mathml:annotation> and <mathml:annotation-xml> elements.
An example demonstrating the embedding of MathML content and presentation markup elements in a CellML document is presented in Section 4.3.
4.2.3 The CellML subset of MathML content elements
Valid CellML documents may contain any MathML content markup elements within a <mathml:math> element, as long as the arrangement of these elements follows the rules defined in the MathML 2.0 Recommendation. However, it is anticipated that it will be some time before software is able to interpret all of these elements. To encourage interoperability, this section defines a subset of the MathML content markup elements known as the CellML subset. CellML documents that only contain content markup elements from the CellML subset are known as valid CellML subset documents. CellML processing software may only call itself CellML conformant if it is able to correctly interpret all of the MathML elements in the CellML subset according to the semantics defined in the MathML 2.0 Recommendation.
The complete list of MathML elements in the CellML subset is given in Figure 5. Many of the elements in the CellML subset are included to provide facilities for the definition of algebraic and ordinary differential equations. Others (such as the trigonometric operators) have been included because they are reasonably straightforward to translate to computer code.
token elements
<cn>,<ci>
basic content elements
<apply>,<piecewise>,<piece>,<otherwise>
relational operators
<eq>,<neq>,<gt>,<lt>,<geq>,<leq>
arithmetic operators
<plus>,<minus>,<times>,<divide>,<power>,<root>,<abs>,<exp>,<ln>,<log>,<floor>,<ceiling>,<factorial>
logical operators
<and>,<or>,<xor>,<not>
calculus elements
<diff>
qualifier elements
<degree>,<bvar>,<logbase>
trigonometric operators
<sin>,<cos>,<tan>,<sec>,<csc>,<cot>,<sinh>,<cosh>,<tanh>,<sech>,<csch>,<coth>,<arcsin>,<arccos>,<arctan>,<arccosh>,<arccot>,<arccoth>,<arccsc>,<arccsch>,<arcsec>,<arcsech>,<arcsinh>,<arctanh>
constants
<true>,<false>,<notanumber>,<pi>,<infinity>,<exponentiale>
semantics and annotation elements
<semantics>,<annotation>,<annotation-xml>
Figure 5 The CellML subset of MathML content markup elements, grouped according to function. All elements in this figure are in the MathML namespace.
4.2.4 Ordering of expressions
The mathematics in a model defined using CellML 1.1 consist of a static system of expressions, which are distributed over a network of components. CellML does not define the order of evaluation of equations, as this is simulation information rather than model information.
4.2.5 Scope of expressions
Within a CellML model, all expressions are assumed to have unlimited scope with respect to the independent variables unless explicitly stated using MathML's <piecewise> construct or some other form of conditional expression. This means that if the initial conditions for a variable, the value of which is determined by a differential equation, are to be specified using an equality, the two equations should have their scope limited so that they do not contradict each other.
4.2.6 Associating units with numbers
To ensure that models are robust and portable, all variables and numbers that occur in mathematical expressions within a CellML document must have units associated with them. CellML's units framework is introduced in Section 5 and the association of units with variables is presented in Section 3.2.3. The association of units with numbers in equations requires an extension to MathML. This can be done in a manner consistent with the association of units with variables and with application-specific extensions to CellML by adding a units attribute in the CellML namespace to the <mathml:cn> element, which encloses all numbers. The example presented in Section 4.3 demonstrates this.
4.2.7 Definition of scripts
CellML 1.1 does not define a standard method by which model authors can embed scripts in CellML documents in a portable way. It is anticipated that this functionality will be defined in a subsequent version of CellML. However, the use of scripts in CellML is strongly discouraged. CellML is aimed at specifying a model in terms of its most basic governing equations. Wherever possible, mathematical equations should be used to specify the changing behaviour of a model's state variables.
If implementors do decide to add scripting functionality to CellML documents, these scripts must be defined within elements placed in an application-specific extension namespace. Implementors are advised to follow the recommendations on the best practices for embedding and executing scripts described in Appendix B. The key recommendations are summarised in the following list:
- For interoperability, scripts should be defined using ECMAScript.
- The
<mathml:csymbol>element should be used from within MathML markup to call scripts defined using a non-MathML syntax. These elements must define adefinitionURLthat identifies the element containing the script and anencodingattribute specifying the scripting language used. - Function names (or the identifier used to reference a script) should be valid CellML identifiers, as defined in Section 2.2.1.
- The content of a
<mathml:csymbol>element should be a human-readable identifier for the script, preferably the function name. - Functions must be side-effect free. That is, a function must not assign values to variables that are not local to that function. In particular, functions must not alter the values of their arguments or global variables.
4.3 Examples
The CellML fragment in Figure 6 demonstrates how MathML can be employed within CellML to define mathematical expressions. This fragment is part of the definition of a component that represents the behaviour of the n gate from the potassium channel in the Hodgkin-Huxley squid axon model of 1952. The component contains three units definitions (with syntax defined in Section 5), two variable declarations (with syntax defined in Section 3), and a block of MathML that defines an expression calculating the alpha variable of the n gate as well as the rendering of this equation, which is given in Equation 2.
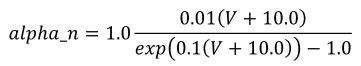 |
(2) |
Figure 6 Part of the definition of a component that represents the behaviour of the n gate from the potassium channel in the Hodgkin-Huxley squid axon model of 1952. See text for more details.
Content that isn't defined using the MathML content markup elements can be associated with a MathML expression using the <mathml:semantics>, <mathml:annotation> and <mathml:annotation-xml> elements. The first child of a <mathml:semantics> element is the expression to be annotated, and the subsequent <mathml:annotation> and <mathml:annotation-xml> elements contain character data and XML annotations, respectively. In the CellML fragment in Figure 6, the expression of interest has been annotated with rendering information encoded using the MathML presentation markup elements. The MathML presentation elements are very flexible and it is possible to produce the same rendering of an equation in many ways — the choice of elements in Figure 6 is somewhat arbitrary.
The <mathml:apply> element at the top level of the expression defines an id attribute, which can be used to associate further metadata with the expression. The linking of metadata with elements in a CellML document is described in more detail in Section 8.2.
All of the <mathml:cn> elements in the equation define cellml:units attributes, which associate a units definition with the number delimited by the <mathml:cn> element. The inclusion of units in the equation allows CellML processing software to check that the dimensions of the terms in an equation are consistent, as discussed in Section 5. The presence of the unit scale factor on the right hand side of the equation is needed for the equation to have consistent dimensions.
4.4 Rules for CellML Documents
4.4.1 The <mathml:math> element
- Allowed use of the
<mathml:math>element- The
<mathml:math>element must only appear as a child of the following elements in the CellML namespace:<cellml:component>and<cellml:role>. [ In this and subsequent rules, the use of themathmlandcellmlnamespace prefixes indicates that elements and attributes are in the MathML and CellML namespaces, respectively. The<mathml:math>element may appear inside elements in the RDF and CellML Metadata namespaces if permitted by the relevant specifications, and may be used inside extension elements. When MathML elements occur within extension elements, CellML processing software is free to ignore them. ] - All elements in the MathML namespace that are within a
<mathml:math>element, and not within a<mathml:annotation>or<mathml:annotation-xml>element, must be taken from the complete set of MathML content markup elements, as defined in Section 4.4 of the MathML 2.0 Recommendation, with the addition of the<mathml:logbase>element. [ CellML only makes use of the content markup elements from MathML. However presentation markup elements may be used within the annotation elements to associate rendering information with expressions. The<mathml:logbase>element was erroneously omitted from the list of content markup elements in Section 4.4 of the MathML 2.0 Recommendation. ] - The content of a
<mathml:math>element must conform to the MathML 2.0 Recommendation from the W3C. - For interoperability, all elements in the MathML namespace that are within a
<mathml:math>element, and not within a<mathml:annotation>or<mathml:annotation-xml>element should be taken from the CellML subset of MathML content markup elements defined in Figure 5. [ The CellML subset is discussed further in Section 4.2.3. Note that this is an interoperability recommendation and not a firm rule. ]
- The
4.4.2 The <mathml:ci> element
- Allowed use of the
<mathml:ci>element- After leading and trailing whitespace is removed, the content of a
<mathml:ci>element must match the value of the name of a variable declared within the current component. [ The<mathml:ci>element is used to reference variables from inside equations. Whitespace may be added before and/or after a variable's name to make the MathML more readable. The handling of whitespace in MathML is described in more detail in Section 2.4.6 of the MathML 2.0 Recommendation. ]
- After leading and trailing whitespace is removed, the content of a
4.4.3 The <mathml:cn> element
- Allowed use of the
<mathml:cn>element- A
<mathml:cn>element must define acellml:unitsattribute. [ All bare numbers in MathML content markup are enclosed in a<mathml:cn>element in the MathML namespace. ]
- A
- Allowed values of the
cellml:unitsattribute- The value of the
cellml:unitsattribute must be taken from the standard dictionary of units given in Section 5.2.1, or be the value of thenameattribute on a<cellml:units>element defined in the current<cellml:component>or<cellml:model>element.
- The value of the
4.4.4 Modification of variables
- A mathematical expression defined using MathML must only modify the values of variables that belong to the current component. [ Variables that belong to a component are those that are not declared with a
public_interfaceorprivate_interfaceattribute value of"in". ]
4.5 Rules for Processor Behaviour
4.5.1 Ordering of expressions
CellML processing software must not assume that the ordering of expressions within a CellML document has any significance.
4.5.2 Scope of expressions
CellML processing software must make no assumptions about the scope or domain of a mathematical expression defined within a model. Unless explicitly stated, all expressions hold for any and all combinations of independent variables.
4.5.3 Treatment of annotations
CellML processing software must assume that the content of the first child of a <mathml:semantics> element defines an expression describing the mathematical behaviour of the model. CellML processing software may ignore the content of <mathml:annotation> and <mathml:annotation-xml> elements.
5 Units
5.1 Introduction
One of the key features ensuring robustness and re-usability of CellML components and models is the requirement that units be associated with all variables and numbers in a CellML document. This allows components and models that declare variables with different units to be connected, as long as variables that are mapped to one another have the same dimensions. For instance, it is possible to map a variable declared with units of "pound/foot" to a variable declared with units of "kilogram/metre", but not to a variable declared with units of "mole/litre" or "kilogram-squared/metre". The explicit declaration of units also allows CellML processing software to check the consistency of each equation in a model.
5.2 Basic Structure
5.2.1 Dictionary of standard units
CellML provides a dictionary of standard units that may be used in variable declarations or attached to bare numbers in mathematics. References to these units should make use of the actual name of the units, rather than the standard abbreviation, thus avoiding confusion between units (e.g., metre) and prefixes (e.g., milli). The full list of units that any CellML processing application is expected to recognise is given in Table 2. The keywords in the table comprise the SI base units, the SI derived units with special names and symbols, and some additional units commonly used in the types of biological models likely to be defined using CellML.
| ampere | farad | katal | lux | pascal | tesla |
| becquerel | gram | kelvin | meter | radian | volt |
| candela | gray | kilogram | metre | second | watt |
| celsius | henry | liter | mole | siemens | weber |
| coulomb | hertz | litre | newton | sievert | |
| dimensionless | joule | lumen | ohm | steradian |
Table 2 The dictionary of units keywords that CellML processing applications are expected to recognise. Base SI units are printed in bold text, derived SI units are printed in plain text, and additions to the standard units defined purely for the convenience of model authors are italicised.
The SI base units are the foundation of the units system in CellML. The conversion of a variable's value between two sets of units involves the expansion of all units definitions to linear combinations of the SI base units and user-defined base units (described in Section 5.2.3). The list of SI base and derived units is taken from The International System of Units (SI), including the Year 2000 Supplement. The American spellings of meter and liter are taken from the NIST Guide for the Use of the International System of UNITS (SI). The SI standard defines the mathematical relationships between the SI derived units and the SI base units. These relationships are given in the right hand column of Table 3 in the Year 2000 Supplement, with the exception of celsius, which is related to kelvin as described in Section 2.1.1.5 of the SI standard.
The CellML units dictionary includes four non-SI units definitions for the convenience of modellers: dimensionless, gram, liter and litre. The only unfamiliar name on this list is dimensionless, which is used to indicate that a number or variable has no units associated with it. The mathematical relationships between gram and litre and the base SI units are given in Section 5.2.5.
5.2.2 User defined units
CellML also provides a facility whereby new units can be defined in terms of the units provided in the dictionary. This functionality allows the definition of units which are expressed as a scaled version of other units (as is the case for most imperial units), the definition of units which are made up of the product of other units, and even the creation of units that require an offset, such as degrees Fahrenheit. This allows model authors to work in whatever set of units they feel most comfortable, while still ensuring that their models can be integrated with those of other authors using different units.
New units are defined or declared using the <units> element, which may be placed inside <model>, <import>, and <component> elements. When a <units> element is placed inside the <model> or <import> element, the units definition may be referenced from within any component in the model. When a <units> element is placed inside a <component> element, the units definition may only be referenced from within that component.
Each units element must define a name attribute, which is used to reference the units definition elsewhere. The value of the name attribute on a <units> element defined in a <model> element or declared in an <import> element must be unique across all <units> elements in the <model> and all <import> elements. For <units> elements defined in a <component> element, the value of the name attribute must be unique across all <units> elements in the <component> in which it is defined. If the value of the name attribute of a <units> element defined inside a <component> element matches the value of the name attribute on a <units> element defined inside the <model> or an <import> element, then it will redefine the units, and all references to these units within the <component> element refer to the new definition. Model authors must not redefine any of the standard units. Therefore, the value of the name attribute must not equal one of the names from the standard units dictionary in Table 2.
A units declaration appearing directly inside an <import> element must also define a units_ref attribute, which is described in Section 9. A units definition appearing directly inside a <model> or <component> element may also define a base_units attribute, the associated behaviour of which is discussed in Section 5.2.3, and may contain a set of <unit> elements that reference units from the dictionary or some previously defined units.
A <unit> element must not contain any elements in the CellML namespace, but may have up to five attributes. The units attribute is the only one that is required. It is used to set the base quantity for the current <unit> element, and its value must correspond to a keyword from the standard CellML units dictionary or to the value of the name attribute of a <units> element in the current component or model.
The definition of new units in terms of subunits may require the use of some combination of the optional offset, prefix, exponent, and multiplier attributes.
A multiplier attribute can be used to pre-multiply the quantity to be converted by any real scale factor. For instance, a multiplier of 0.45359237 is used to define a pound in terms of a kilogram. The multiplier attribute has a default value of "1.0"
The offset attribute is used to represent the addition of a constant in the transformation between the current units and the base units. This should only be necessary for the definition of temperature scales. For instance, an offset attribute value of "32.0" is needed to define Fahrenheit in terms of Celsius. The offset attribute has a default value of "0.0".
The prefix attribute can be used to indicate a scale for the referenced units. It is included primarily for the convenience of modellers who want to define units that differ from another units definition only by an SI scale factor. Its value must be from the standard set of CellML prefix names given in Table 3 or be an integer, in which case the units are pre-multiplied by 10 to the power of this number. The default value of the prefix attribute is "0" (the referenced units are scaled by a factor of one).
| name | factor | name | factor |
|---|---|---|---|
| yotta | 1024 | deci | 10-1 |
| zetta | 1021 | centi | 10-2 |
| exa | 1018 | milli | 10-3 |
| peta | 1015 | micro | 10-6 |
| tera | 1012 | nano | 10-9 |
| giga | 109 | pico | 10-12 |
| mega | 106 | femto | 10-15 |
| kilo | 103 | atto | 10-18 |
| hecto | 102 | zepto | 10-21 |
| deka | 101 | yocto | 10-24 |
Table 3 The set of names that may be used in the prefix attribute on a <unit> element and the corresponding scale factors that will pre-multiply the unit.
The scale factor described by the prefix attribute and the units referenced by the units attribute are raised to a power equal to the value of the exponent attribute. The value of the exponent attribute must be a floating point number, and is typically an integer. The exponent attribute has a default value of "1.0". Note that an exponent attribute value of "0.0" has the effect of removing the parent <unit> element from the current units definition.
A simple units definition occurs when units are defined as a linear function of some previously defined simple units or base units. In a simple units definition, a <units> element contains only a single child <unit> element, that <unit> element has an exponent attribute value of "1.0", and the units definition referenced by the units attribute is one of the SI or user-defined base units or is itself a simple units definition. These are the only conditions under which a <unit> element may define an offset attribute with a value other than "0.0". The formula that expresses how the old units (referenced by the value of the units attribute on the <unit> element) are transformed into the new units (defined by the value of the name attribute on the parent <units> element) is given below.
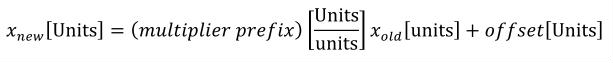 |
(3) |
Terms in square brackets represent the units associated with values in the expression, which are italicised. xold is the value to be transformed from the old units, and xnew is the resulting value in the new units. Units are the units being defined, and multiplier, prefix, units and offset correspond to the values of the appropriate attributes on the <unit> element.
Complex units are the product of multiple units. In a complex units definition, a <units> element contains more than one <unit> element or a <unit> element that defines an exponent attribute with a value other than "1.0". The conversion between the new units and the product of the constituent units is given by the formula below.
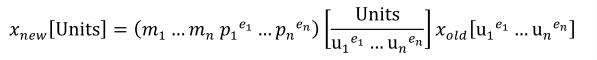 |
(4) |
The mi, pi, ui, and ei terms refer to the values of the multiplier, prefix, units and exponent attributes on the i-th <unit> element respectively.
An offset attribute may not be defined on any <unit> elements that occur inside a complex units definition. When a complex units definition references a simple units definition, any offset associated with the simple units definition is removed. This means that conversions such as the one between degrees Fahrenheit per inch and degrees Celsius per centimetre involve only a scale factor.
5.2.3 New base units
A modeller might want to define and use units for which no simple conversion to SI units exist. A good example of this is pH, which is dimensionless, but uses a log scale. Ideally, pH should not simply be defined as dimensionless because software might then attempt to map variables defined with units of pH to any other dimensionless variables.
CellML addresses this by allowing the model author to indicate that a units definition is a new type of base unit, the definition of which cannot be resolved into simpler subunits. This is done by defining a base_units attribute value of "yes" on the <units> element. This element must then be left empty. The base_units attribute is optional and has a default value of "no". If the base_units attribute is omitted or assigned a value of "no", units are expected to be defined in terms of other units as described in Section 5.2.2.
The indiscriminate use of the base_units attribute is strongly discouraged, because it has a significant impact on the re-usability of models and components. In particular, the base_units attribute should not be used to restrict users to creating models with an application-specific dictionary of units, as this prevents the efficient exchange of CellML models with other applications.
Software that is checking the consistency of the units in an equation (described in more detail in Section 5.2.7) can stop the recursive resolution of units definitions when the only remaining units are base SI units and user-defined base units.
5.2.4 Expansion of units definitions
For interoperability, software that claims to perform units conversion when passing variables between components and/or claims to perform dimension consistency checking of equations should obtain results that are equivalent to those produced using the algorithms described in Appendix C.3.5 and Appendix C.3.6, respectively. Both of these algorithms make use of the algorithm defined in Appendix C.3.4 to fully expand units definitions into functions of the SI and user-defined base units.
For both simple and complex units definitions (as defined by Equation 3 and Equation 4, respectively), the algorithm recursively substitutes in equations expanding the unknown term xold, stopping when the unknown term has only SI or user-defined base units.
Although this specification does not require software to implement this algorithm exactly, it is used extensively to demonstrate units conversion and dimension checking as described in Section 5.2.6 and Section 5.2.7, respectively. Appendix C.4.2 provides examples of units definition expansion according to the algorithm described in Appendix C.3.4.
5.2.5 Expansion of the non-SI units definitions in the CellML dictionary
Having defined a mathematical notation in Section 5.2.2 and a technique for the expansion of units definitions, it is now possible to formally specify how the definitions of the non-SI units in Table 2 should be expanded. The CellML versions of these units definitions and the associated equations are given below. The definition of liter is identical to the definition of litre. As described in Section 5.2, dimensionless is not related to the SI units and cannot be expanded.
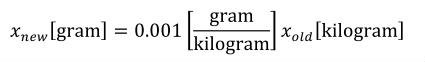 |
(5) |
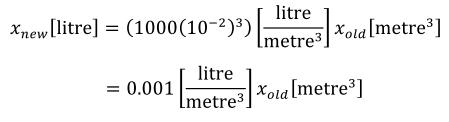 |
(6) |
5.2.6 Conversion between units definitions
Associating units definitions with every variable declaration in a component allows variables from components that make use of different sets of units to be mapped together, as long as the variables have the same dimensions. Appendix C.3.5 specifies a possible method for converting a numeric value from one set of units to another. CellML processing software is not required to be capable of converting between units definitions. However, for interoperability, software that does implement this functionality should achieve the same results as if this method were used, although the exact implementation may differ.
This implementation generates an expression that relates each units definition to SI and user-defined base units. This expression is obtained by recursively expanding each units definition as described in Appendix C.3.4, and then simplifying the result. The expression for the input units is then inverted to give an expression that relates the appropriate base units to the input units. This inverted expression is substituted into the expression for the target units, producing a single expression that relates the quantity to be converted from the input units to a corresponding quantity in the target units. The inversion and substitution process is demonstrated by example in Appendix C.4.3.
5.2.7 Equation dimension checking
The association of units with every variable and bare number that appears in an equation in a CellML document provides CellML processing software the opportunity to perform equation dimension checking. Verifying that equations have consistent dimensions can potentially catch many basic mathematical errors.
Appendix C.3.6 specifies a possible implementation of equation dimension checking. This implementation splits an equation into a tree of equation parts, in which each parent part is obtained by the application of a single operator to its children. The units definition on each leaf node (i.e., part without children) is expanded into base units, as described in Appendix C.3.4. The units definition for a node at a higher level of the tree is constructed by combining the units definitions of its children. An equation has consistent dimensions if no errors are found while traversing the tree and if the fully expanded units definitions of the two nodes at the top level of the tree are equivalent, as defined in Appendix C.2.2.
CellML processing software is free to ignore units in mathematics and assume that equations are consistent. For interoperability, software that performs equation dimension checking should achieve the same results as if the implementation discussed in Appendix C.3.6 were used, although the exact implementation may differ.
This specification does not attempt to completely prevent model authors from creating invalid mathematics. Dimension consistency checking prevents modellers from adding variables with different dimensions but would not find errors in Equation 7 and Equation 8, which have different units but the same dimensions:
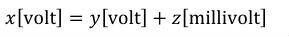 |
(7) |
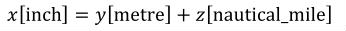 |
(8) |
Although it would be technically possible (and useful) to find and correct such errors, CellML processing software is not required to be able to do so.
5.3 Examples
5.3.1 User-defined units and new base units
Figure 7 demonstrates how users can extend the set of units in the CellML dictionary by defining new sets of units.
Figure 7 Some examples of the use of the <units> element demonstrating the definition of simple and complex units.
5.3.2 Advanced examples
Examples of the expansions of units definitions, conversion between units definitions and equation dimension checking are given in Appendix C.4.
5.4 Rules for CellML Documents
Units are a fundamental part of a CellML model definition. In this section, formal rules are specified for the system of units definition introduced in Section 5.2.
5.4.1 The <units> element
- Allowed use of the
<units>element- The
<model>,<import>and<component>elements may contain any number of<units>elements. - Each
<units>element must define anameattribute. - Each
<units>element appearing as the child of a<model>or<component>element may also define abase_unitsattribute. [ Units declared in an<import>element are not new definitions, and therefore can't be defined as base units. ] - If a
<units>element appearing as the child of a<model>or<component>element defines abase_unitsattribute with a value of"yes", then that<units>element must contain only the following elements, which may appear in any order:<RDF>elements in the RDF namespace.
- If a
<units>element appearing as the child of a<model>or<component>element does not define abase_unitsattribute with a value of"yes", then that<units>element must contain only the following elements, which may appear in any order:<unit>elements in the CellML namespace,<RDF>elements in the RDF namespace.
- Each
<units>element appearing as the child of an<import>element must also define aunits_refattribute. - A
<units>element appearing as the child of an<import>element must contain only the following elements, which may appear in any order:<RDF>elements in the RDF namespace.
- The
- Allowed values of the
nameattribute- The value of the
nameattribute must be a valid CellML identifier as discussed in Section 2.2.1. - The value of the
nameattribute must not equal one of the names defined in the standard dictionary of units in Table 2. [ Model authors may not redefine the standard units. ] - For units defined in a
<model>element or declared in an<import>element, the value of thenameattribute must be unique across all<units>elements within the<model>and all<import>elements. For units defined in a<component>element, the value of thenameattribute must be unique within the given<component>element. [ Two<units>elements in the<model>and<import>elements may not have the samenameattribute value, although a<units>element in a<component>element may share the same name as a<units>element in the<model>element or<import>elements. In this case, the units definition in the<component>element supersedes the model-wide definition when referenced inside that component. ]
- The value of the
- Allowed values of the
base_unitsattribute- If present, the value of the
base_unitsattribute must be"yes"or"no". - If not present, the value of the
base_unitsattribute defaults to"no".
- If present, the value of the
- Proper use of the
base_unitsattribute- A
base_unitsattribute must not be defined on a<units>element appearing as a child of an<import>element.
- A
5.4.2 The <unit> element
- Allowed values of the
units_refattribute- The value of the
units_refattribute must equal the value of the name attribute of a<units>element defined in the model at the URI given on the parent<import>element.
- The value of the
- Proper use of the
units_refattribute- A
units_refattribute must not be defined on a<units>element appearing as a child of a<model>element or a<component>element. [ Aunits_refattribute would have no meaning on a units definition. ]
- A
5.4.3 The <unit> element
- Allowed use of the
<unit>element- A
<unit>element must contain only the following elements:<RDF>elements in the RDF namespace.
- Each
<unit>element must define aunitsattribute. It may also defineprefix,exponent,multiplier, andoffsetattributes.
- A
- Allowed values of the
unitsattribute- The value of the
unitsattribute must be taken from the standard dictionary of units listed in Table 2 or be the value of thenameattribute on a<units>element defined in the current<component>or<model>element. - The value of the
unitsattribute must not reference a units definition that contains<unit>elements that in turn directly or indirectly reference the current units definition. [ This rule prevents circular units definitions. It must be possible to break down a complex units definition into SI and user-defined base units. ]
- The value of the
- Allowed values of the
prefixattribute- If present, the value of the
prefixattribute must be an integer or a name taken from one of the name columns of Table 3. [ The unit is scaled by 10 raised to the power of the specified integer or the factor corresponding to the specified name. Therefore,prefixattribute values of"centi"and"-2"are equivalent. ] - If not present, the value of the
prefixattribute defaults to"0".
- If present, the value of the
- Allowed values of the
exponentattribute- If present, the value of the
exponentattribute must be a real number. - If not present, the value of the
exponentattribute defaults to"1.0".
- If present, the value of the
- Allowed values of the
multiplierattribute- If present, the value of the
multiplierattribute must be a real number. - If not present, the value of the
multiplierattribute defaults to"1.0".
- If present, the value of the
- Allowed values of the
offsetattribute- If present, the value of the
offsetattribute must be a real number. - If not present, the value of the
offsetattribute defaults to"0.0".
- If present, the value of the
- Proper use of the
offsetattribute- A
<units>element containing a<unit>element that defines anoffsetattribute with a value other than"0.0"must not contain other<unit>elements. [ Theoffsetattribute can only be used in a simple units definition, as defined in Section 5.2.2. ] - A
<unit>element that defines anoffsetattribute with a value other than"0.0"must not define anexponentattribute with a value other than"1.0". [ Theoffsetattribute can only be used in a simple units definition, as defined in Section 5.2.2. ]
- A
5.5 Rules for Processor Behaviour
5.5.1 Resolving references to units definitions
The <units> element may be placed inside <model>, <import>, and <component> elements. When user-defined units are referenced by a variable or number declaration inside a component, the units definition is first looked for inside the current <component> element. If a matching units definition cannot be found, then the units definition is looked for in the <model> element and <import> elements.
5.5.2 Units associated with the MathML constants elements
This section defines the units associated with the MathML elements that appear in the constants subset of the CellML set defined in Section 4.2.3. These elements represent numerical values. Operators can be applied to combinations of these elements, variables and numbers in an equation. Units must be associated with these elements to allow for equation dimension checking.
The <true> and <false> elements have units of cellml:boolean, where cellml:boolean is a set of base units defined purely for use in this specification. (Note that users may not define their own cellml:boolean units, as this is not a valid CellML identifier.) cellml:boolean units are not associated with variables or numbers, but can be produced as the result of the application of relational or logical operators, as discussed in Appendix C.3.3.
The <notanumber>, <pi>, <infinity> and <exponentiale> elements all have units of dimensionless.
6 Grouping
6.1 Introduction
It is often useful to organise groups of components within a model into a hierarchical structure. This structure might reflect a logical organisation of components within the group or their physical configuration. CellML provides a single mechanism for the specification of both of these types of hierarchy that is based on a grouping scheme. This grouping scheme is general enough that it can be used within CellML documents to specify non-hierarchical grouping relationships between components.
In CellML, a hierarchy is a tree of components linked by parent-child relationships, where all of these relationships are of the same type. A hierarchy has a single root component and at least one child component. A model may contain numerous hierarchies of the same type. A component must only appear once within a set of hierarchies of a given type, but may appear in multiple hierarchies if each of these hierarchies is of a different type. CellML defines two types of relationship for use within the grouping scheme: encapsulation and containment.
The definition of a logical hierarchy of components in a network is known as "encapsulation". Encapsulation allows the modeller to hide part of a model by using a single component as an interface to a hidden submodel. The parent component hides the details of one or more child components from the rest of the model. Encapsulation provides a powerful mechanism for simplifying the structure of the model by preventing connections between specified sets of components. Components in the main model must not be connected to child components in the encapsulated submodel — all variables must be mapped through the encapsulating parent component. A component in the submodel must only be connected to its parent component, other components in the same submodel, and components that it encapsulates. A modeller wishing to reuse an encapsulated submodel may treat the submodel as a "black box", and deal exclusively with the interface presented by the encapsulating component.
The definition of physical hierarchies within a model is known as "containment". A model author can specify that one or more child components are physically inside of a parent component without describing the geometric aspects of the relationship in detail. This information would typically be used by CellML processing software to provide a physical representation of a model. A model may contain multiple types of containment hierarchy, which are differentiated based on names that the modeller assigns to these hierarchies.
Model authors are also free to extend the grouping scheme with user-defined types of relationships between components. These relationships need not be hierarchical in nature. However, CellML processing software is only required to recognise encapsulation and containment relationships.
Encapsulation and containment hierarchies do not add any mathematical information to the model. Model authors must not define their own grouping relationships that are intended to imply mathematical information.
Models may define multiple hierarchies of multiple types. CellML processing software is free to treat all hierarchies of the same type as separate hierarchies. Alternatively, it may combine all hierarchies of the same type into a single hierarchy by assuming that the root components of all explicitly defined hierarchies are children of a single anonymous component. This anonymous component is not explicitly defined within the CellML document and has no properties.
6.2 Basic Structure
6.2.1 Definition of groups
Logical and physical hierarchies are both declared using the <group> element. This element must be a child of a <model> element. A <group> element can be used to define multiple hierarchies and associate multiple relationship types with each hierarchy. The definition of a hierarchy or set of hierarchies of the same type can be split up over multiple <group> elements, as long as all the children of a given parent component in a hierarchy appear in a single <group> element.
A <group> element must contain one or more <relationship_ref> elements, each of which must define a relationship attribute, the value of which references one type of relationship. CellML processing software is required to recognise two types of relationship: encapsulation and containment, which are indicated by relationship attribute values of "encapsulation" and "containment", respectively. Model authors can define new types of relationship by specifying a relationship attribute that is not in the CellML namespace on the <relationship_ref> element. All of the relationships referenced by the <relationship_ref> elements within a given <group> element are associated with all the parent-child pairs defined within that <group> element.
A <group> element must also contain one or more <component_ref> elements. Each <component_ref> element must define a component attribute, the value of which references a component within the current model. A parent-child link is created between components by nesting a <component_ref> element that references the child component inside a <component_ref> element that references the parent component. Multiple levels of nesting may be used within a single <group> element to define a hierarchy.
All <component_ref> elements defined immediately inside the <group> element must contain further <component_ref> elements when defining an encapsulation or containment hierarchy. This ensures that valid hierarchical structures are defined. Top-level <component_ref> elements need not contain further <component_ref> elements in <group> elements that reference only user-defined relationships. This allows the definition of non-hierarchical relationships.
A single hierarchy may be defined in multiple <group> elements. This occurs when a component is referenced in two groups that reference the same relationship type. However, all of the children of a given parent component must be defined within a single <group> element. Therefore, any given component can only be referenced once as a parent and once as a child for a given relationship type across the entire model. This simplifies the construction and validation of hierarchies.
A <relationship_ref> element may define a name attribute in addition to the required relationship attribute. The value of the name attribute on <relationship_ref> elements can be used to refine a given relationship type. This allows, for instance, the creation of several overlapping containment hierarchies within the same model, each with a different name. See Section 6.2.4 for more information on this.
Geometric containment relationship information is formally independent of logical encapsulation information, but CellML processing software is free to check for inconsistencies between the two relationships — it would generally be an error for an encapsulating component to be physically inside one of its encapsulated child components.
6.2.2 The encapsulation relationship type
Encapsulation allows the modeller to split a model into layers of complexity. A single component can be used to encapsulate a complex partial model, and thereby provide a unified interface for all information passing between that submodel and the rest of the model. This allows a modeller to refine the encapsulated submodel without having to make any changes to the rest of the model.
A model may contain any number of encapsulation hierarchies, as long as these do not overlap. If more than one hierarchy is explicitly defined, it may be useful to combine these into a single hierarchy by assigning all unencapsulated components an anonymous parent component. This anonymous component could make it easier to check that the hierarchies do not overlap and do not define any circular relationships between components.
The components in a model can be divided into four sets with respect to any given component (the current component). The set of all components immediately encapsulated by the current component is the encapsulated set. The parent component is the component that encapsulates the current component. Other components encapsulated by the same parent make up the sibling set. All other components, which are not available to make connections with the current component, make up the hidden set. If the current component is not encapsulated, then it has no parent and the sibling set consists of all other unencapsulated components in the model.
These sets are best demonstrated by example. Given the network shown in Figure 8, Table 4 lists the parent components and the components in the encapsulated, sibling, and hidden sets for a selected set of components picked as the current component.
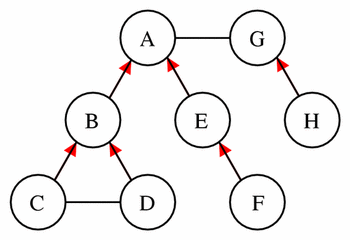
Figure 8 This simple model provides the basis for the demonstration of the concepts of encapsulated sets, parents, sibling sets, and hidden sets, as described in the text. The model consists of eight components each represented by a circle. The lines between the components represent connections, and a red arrowhead on one of these lines indicates that the component at the tail of the arrow is encapsulated by the component at the head of the arrow.
| Current Component | Encapsulated Set | Parent | Sibling Set | Hidden Set |
|---|---|---|---|---|
| A | B, E | anonymous | G | C, D, F, H |
| B | C, D | A | E | F, G, H |
| C | none | B | D | A, E, F, G, H |
| E | F | A | B | C, D, G, H |
| G | H | anonymous | A | B, C, D, E, F |
Table 4 This table lists the parent components, and the components in the encapsulated, sibling, and hidden sets for a selected few components from the example model in Figure 8. Components A and G are root components of separate hierarchies. It may be useful, however, to assign them an anonymous parent component that enables the formation of a single encapsulation hierarchy for the entire model.
Every variable must define its availability for use in other components. This is done with the public_interface and private_interface attributes on the <variable> element. The interface exposed to the parent component and components in the sibling set is defined by the public_interface attribute. The private_interface attribute defines the interface exposed to components in the encapsulated set. Each interface has three possible values: "in", "out", and "none", where "none" indicates the absence of an interface. The separation of interfaces allows the modeller to incrementally add complexity to an encapsulated submodel without changing the interface that the encapsulating component presents to the rest of the model.
The mappings allowed between variables declared in each component are defined by the public and private interfaces of each variable and the prohibition on connecting an encapsulated component to components other than its parent component, members of its sibling set, and any components it in turn encapsulates. Variables with a public_interface attribute value of "in" must be mapped to a single variable in a component in the encapsulated or sibling sets with a public_interface attribute value of "out" or to a single variable in the parent of the current component with a private_interface attribute value of "out". Similarly, variables with a public_interface value of "out" may be mapped to variables in components in the encapsulated or sibling sets with a public_interface attribute value of "in" or to variables in the parent component with a private_interface value of "in". Note that defining a public_interface attribute value of "out" on a variable makes it legal to map the variable to other variables, but does not require that such a mapping occur. If a variable has a public_interface attribute value of "none", it is neither input from or exposed to its parent or components in the sibling set.
Variables with a private_interface attribute value of "in" must be mapped to a single variable in a single component in the encapsulated set with a public_interface attribute value of "out". Variables with a private_interface attribute value of "out" may be mapped to variables in components in the encapsulated set with a public_interface attribute value of "in". If a variable has a private_interface attribute value of "none", it is neither input from or exposed to the components in the encapsulated set.
If either the public_interface attribute or the private_interface attribute of a variable have a value of "in", that variable is declared elsewhere and its value must not be mathematically modified in the current component. Otherwise, the variable belongs to the current component. If both the public_interface and private_interface attributes of a variable have a value of "none", the variable can only be used in the current component and is invisible to all other components in the model.
The two interface attributes of a variable are completely independent with one exception: it is invalid for a variable to have both public_interface and private_interface attributes with a value of "in". An interface with a value of "in" reflects an unmet need in the current component that must be satisfied — this need can be met in either the public or private interface, but not both.
6.2.3 The containment relationship type
The containment relationship allows the modeller to specify that a particular component is physically inside another. This might be used by software to create a physical representation of the model. Containment relationships can be specified either in combination with or independent of encapsulation relationships. Containment relationships do not influence any aspect of model definition or behaviour.
6.2.4 Named containment relationship types
CellML allows the definition of multiple overlapping containment hierarchies in a given model. This functionality allows the modeller to define several different ways of organising a model, each of which might highlight a different aspect of the model's physical structure.
Multiple containment hierarchies are created by defining name attributes on the <relationship_ref> elements that have relationship attribute values of "containment". In effect, the introduction of a name attribute defines a new relationship type that has the same semantics as the unnamed containment relationship type. All containment hierarchies that share the same name are subject to the same rules that apply to any set of hierarchies that share the same relationship type. That is, each component must be referenced at most once as a parent or child for a given relationship type, and circular hierarchies must not be defined. Note that <group> elements that contain <relationship_ref> elements with a relationship attribute value of "containment" and that do not define a name attribute belong to a single relationship type that is separate from any named containment relationship types.
6.2.5 User-defined relationship types
Modellers are free to use the grouping syntax of CellML to organise model components in ways not defined by the CellML specification. To do this, the model author defines a new relationship type, the name of which is used as the value of the relationship attribute on the <relationship_ref> element. The relationship attribute must be placed in an extension namespace, because future versions of the CellML specification may define additional relationship types, the names of which could otherwise conflict with user-defined relationship types.
User-defined relationship types can be used in the definition of hierarchical relationships and can also be used to define more generic grouping relationships. For example, a modeller may define a relationship type called adjacency, that indicates that any components referenced inside the group are physically adjacent to each other.
Modellers are free to use the name attribute on the <relationship_ref> element to specify multiple hierarchies for user-defined relationship types, as is possible for the containment relationship type.
This specification does not provide a mechanism by which modellers may specify the meaning of a user-defined type of relationship. This definition must be provided by the processing software declaring the new relationship type.
6.3 Examples
Figure 9 demonstrates the use of the <group> element to define an encapsulation relationship. This example is taken from the two reaction pathway with encapsulation example from the examples section of the CellML website. It shows how a component representing an overall reaction (total_reaction) can encapsulate components representing intermediate reactions (first_reaction and second_reaction) and their by-products (C and D).
Figure 9 Example demonstrating the use of the <group> element to define a logical encapsulation relationship. See text for more details.
Figure 10 demonstrates the use of the <group> element to define encapsulation and containment relationships, the construction of two named containment relationship types, and the specification of a custom relationship type (adjacency) in an extension namespace.
Figure 10 Examples demonstrating the use of the <group> element. See text for more details.
The first <group> element states that the cell_membrane component is physically inside the cell component and that this particular containment relationship type is called membrane. The next <group> element states that the sodium_channel and calcium_channel components are both physically inside and logically encapsulated by the cell_membrane component. This containment relationship completes the membrane containment hierarchy. The encapsulation relationship prevents the sodium and calcium channel components from being connected to any components other than the cell_membrane component, each other, and any components they in turn encapsulate.
The third <group> element states that the two components representing parts of the sarcoplasmic reticulum are physically inside the cell, and that this relationship type is called intracellular. Finally, the fourth <group> element introduces the user-defined relationship adjacency and states that the two sarcoplasmic reticulum components share this relationship. This relationship type is declared by putting the relationship attribute in an extension namespace and assigning it a value of "adjacency". Note that this relationship is not hierarchical in nature, and CellML processing software is free to ignore the information provided by this group.
6.4 Rules for CellML Documents
6.4.1 The <group> element
- Allowed use of the
<group>element- A
<model>element may contain any number of<group>elements. - A
<group>element must contain only the following elements, which may appear in any order:-
<relationship_ref>and<component_ref>elements in the CellML namespace, <RDF>elements in the RDF namespace.
<group>element in the order stated above. ] -
- A
<group>element must contain at least one<relationship_ref>element. - A
<group>element must contain at least one<component_ref>element.
- A
6.4.2 The <relationship_ref> element
- Allowed use of the
<relationship_ref>element- A
<relationship_ref>element must contain only the following elements:<RDF>elements in the RDF namespace.
- Each
<relationship_ref>element must define arelationshipattribute in either the CellML namespace or an extension namespace. It may also define anameattribute. [ Arelationshipattribute declaring a user-defined relationship type is placed in an extension namespace. This restriction has been included to prevent conflicts with future versions of the CellML specification, which may define additional types of relationships in the CellML namespace. ]
- A
- Allowed values of the
relationshipattribute- The value of a
relationshipattribute in the CellML namespace must be"containment"or"encapsulation".
- The value of a
- Allowed values of the
nameattribute- The value of the
nameattribute must be a valid CellML identifier as discussed in Section 2.2.1. [ Note that unlike most othernameattributes, the value of thenameattribute on a<relationship_ref>element is not expected to be unique across the current model. Instead,<group>elements that include<relationship_ref>elements that share the samenameattribute value form the parts of a single hierarchy. ]
- The value of the
- Proper use of the
nameattribute- A
nameattribute must not be defined on a<relationship_ref>element with arelationshipattribute value of"encapsulation". [ A model must define at most one unnamed encapsulation hierarchy. ]
- A
- Proper use of the
relationshipandnameattributes[ The following rules together prevent the model author from referencing the same hierarchy more than once within a given
<group>element. ]- A
<group>element must not contain two or more<relationship_ref>elements that define arelationshipattribute in a common namespace with the same value and that have the samenameattribute value. - A
<group>element must not contain two or more<relationship_ref>elements that define arelationshipattribute in a common namespace with the same value and do not definenameattributes.
- A
6.4.3 The <component_ref> element
- Allowed use of the
<component_ref>element- A
<component_ref>element must contain only the following elements, which may appear in any order:<component_ref>elements in the CellML namespace,<RDF>elements in the RDF namespace.
- A
<component_ref>element must define acomponentattribute.
- A
- Proper use of the
<component_ref>element- A
<component_ref>element that is defined immediately within a<group>element that contains a<relationship_ref>element with arelationshipattribute value of"encapsulation"or"containment"must contain at least one child<component_ref>element. [ Containment and encapsulation relationships must be hierarchical. ] - In a given hierarchy, only one of the
<component_ref>elements that reference a given component may contain further<component_ref>elements. [ This rule prevents a given component from being a parent more than once in a given hierarchy. A hierarchy is a set of components linked by a common type of parent-child relationship. The definition of a hierarchy may be split over multiple<group>elements, but the definition of a set of parent-child links must not be. It would be much more difficult to assemble a hierarchy from a CellML document if a set of parent-child links could be defined in multiple<group>elements. ] - In a given hierarchy, only one of the
<component_ref>elements that reference a given component may be contained inside another<component_ref>element. [ Complements the previous rule. This one prevents a given component from being a child more than once in a given hierarchy. ] - In a given hierarchy, a child component must not directly or indirectly contain its parent among its children. [ A hierarchy must not be circular. ]
- A
- Allowed values of the
componentattribute- The value of the
componentattribute must equal the value of thenameattribute of a<component>element contained within the current<model>element.
- The value of the
6.5 Rules for Processor Behaviour
6.5.1 Treatment of relationship types in a single model
A given relationship type must have the same semantics across a model and at all levels in every hierarchy associated with that relationship type. The semantics of the encapsulation and containment relationship types are defined in Section 6.2.2 and Section 6.2.3, respectively.
Within a given <model> element, any hierarchies defined in <group> elements that contain <relationship_ref> elements with identical relationship and name attribute values belong to the same relationship type, and must be treated as such. Any hierarchies defined in <group> elements that contain <relationship_ref> elements with identical relationship attribute values and undefined name attributes belong to the same relationship type, and must be treated as such.
6.5.2 Groups must not imply mathematical information
Modellers must not use CellML groups to add mathematical information to the model. Modellers must not define their own types of relationships that imply mathematical behaviour. This ensures that the mathematical behaviour of a model can be properly reproduced by all CellML processing software.
6.5.3 Groups must not imply metadata information
Modellers must not use CellML groups to associate properties or classification information with sets of components. The metadata functionality is the proper method for making such associations. This increases the chance of that information being used by a range of CellML processing software.
7 Reactions
7.1 Introduction
CellML is intended to be used to represent many different types of models. Therefore, its basic structure is general. Models are primarily specified by explicitly defining mathematics using MathML. It is possible to specify a model purely in terms of mathematics, without using any of the elements defined in this section of the specification. However, in some types of models, information is lost when reducing the model to pure mathematics. For instance, in biochemical pathway models it will not always be straightforward, or even possible, to unambiguously determine from the mathematical rate laws which variables represent inhibitors or activators in the reactions. Therefore, some additional elements are needed in CellML to fully capture the information in biochemical pathway models.
7.1.1 Pathway model representations supported by CellML
Three fundamental representations of reaction/pathway models must be supported by CellML:
- Mathematical Equations: These are any valid mathematical equations that describe the model. For example, they may be ordinary differential equations that define kinetic reaction rate laws and the rate of change of the concentration of species participating in the modelled reactions.
- Chemical Expressions: These are the stoichiometric expressions (such as
A + B <-> 2C + D) used by chemists to represent reactions. - Pathway Diagrams: These are the stylised drawings commonly used by biochemists and cell biologists to represent interactions among participants in reactions. Some examples of pathway diagrams are shown in Section 7.3.
It is important that CellML be able to store the information needed to reproduce unambiguously any of these representations of a model. It is also important to minimise duplication of information within the model definition, because duplication can lead to inconsistencies. Therefore, CellML integrates the information needed to support the three types of model representation.
The integration process has resulted in the introduction of a CellML syntax that implies a mathematical relationship between variables in the current component. In this section of the specification, explicit mathematics refers to equations defined using MathML, and implicit mathematics refers to equations implied from the CellML syntax.
7.1.2 Qualitative and quantitative pathway models
CellML supports both quantitative and qualitative pathway models. Many types of models are commonly referred to as "qualitative". Some of these are mathematically specified, while others are not. For the purposes of this specification, qualitative pathway models consist solely of information about how the different chemical species in the pathway relate, and contain no mathematics. However, the stoichiometry of the reactions may be known. In other words, there is no mathematical representation of the model, but there may still be a pathway diagram and chemical expressions that represent the model. Because a qualitative model has no mathematics, CellML processing software is not required to be able to run a simulation using a qualitative model. However, some software may support simple simulations using such models.
Any model in which the change of concentration of a chemical species participating in a reaction is implicitly or explicitly defined is a quantitative pathway model. All others are qualitative pathway models.
7.2 Basic Structure
The <reaction> element is used to store information associated with a single reaction. It may only appear inside a <component> element. Examples demonstrating the use of the <reaction> element are presented in Section 7.3. It is possible for a single <component> element to contain more than one <reaction> element. However, this makes it difficult to reuse the individual reactions, and is therefore not the recommended best practice. The <reaction> element may define a reversible attribute, the value of which indicates whether or not the reaction is reversible. The default value of the reversible attribute is "yes".
The reaction element contains multiple <variable_ref> elements, each of which references a variable that participates in the reaction. The recommended best practice is to create a <variable_ref> element for each variable representing the concentration of a chemical species that participates in a reaction, as well as one for the variable representing the rate of the reaction. The required variable attribute is the only attribute on the <variable_ref> element. Its value is the name of the referenced variable. This variable must be declared in the current <component> element.
Each <variable_ref> element contains one or more <role> elements. A <role> element must not contain any elements in the CellML namespace, but may have up to four attributes. The required role attribute specifies the way in which the variable participates in the reaction. The role attribute must have a value of "reactant", "product", "catalyst", "activator", "inhibitor", "modifier", or "rate". The meaning associated with each value is defined in Section 7.4. The optional direction attribute may be used on <role> elements in reversible reactions. If defined, it must have a value of "forward", "reverse", or "both". Its value indicates the direction of the reaction for which the role is relevant. It has a default value of "forward". The optional delta_variable attribute indicates which variable is used to store the change in concentration of the species represented by the variable referenced by the current <variable_ref> element. The optional stoichiometry attribute stores the stoichiometry of the current variable relative to the other reaction participants. Section 7.4 contains detailed rules for the use of these attributes.
The <role> elements may also contain <math> elements in the MathML namespace, which define equations using MathML. Although it is not required, it is recommended best practice to store all of the equations that relate to a reaction inside the appropriate <role> elements in the <reaction> element. This makes the <reaction> element more re-usable. In addition, defining mathematics inside a <role> element has the effect of associating the equations with the variable referenced by the containing <variable_ref> element, in the role defined by the <role> element. This enables CellML processing software to present the equations in a more meaningful context. For instance, it may group all of the relationships between the rate variable and the delta variables for all of the reactants and products, or it may display these equations in a different color.
There are three uses for equations inside <role> elements:
- If the
roleattribute value is"rate", any enclosed equations calculate the kinetic rate law (i.e., calculate the value of the referenced variable) and the value of intermediate variables used in the rate law equation. - If the
roleattribute value is"reactant"or"product", the equations calculate the relationship between the general reaction rate and the rate of change of the species represented by the referenced variable (i.e., calculate the value of the variable named in thedelta_variableattribute), and calculate any intermediate variables used in this relationship. - In all other cases, the equations relate an intermediate variable used in the rate calculation to the variable referenced by the containing
<variable_ref>element. For instance, it would be appropriate to calculate an effective concentration of a catalyst inside the<role>element contained by the<variable_ref>element that references the variable representing the actual concentration of the catalyst.
CellML processing software is not required to be able to deduce the stoichiometry of a reaction from explicit mathematics. Therefore, it is strongly recommended that the stoichiometry and delta_variable attributes be used instead of explicit mathematics if the concentration change is simply the reaction rate multiplied by the stoichiometry. (The rules for deriving this mathematical relationship from the stoichiometry attribute are defined in Section 7.5.5.)
7.3 Examples
This section contains two examples demonstrating the recommended use of the <reaction>, <variable_ref> and <role> elements to define two basic reactions. The mathematics defining the reaction rate have been omitted in these examples. See the signal transduction model examples section of the CellML website for further examples.
Figure 11 shows a pathway diagram representation of the following reversible reaction:
A + B <-> 2C + D
Figure 12 demonstrates the use of CellML to define this reaction. There are five <variable_ref> elements in the <reaction> element: one for each variable representing the concentration of a chemical species participating in the reaction, and one for the variable representing the general reaction rate. Note that the stoichiometry attribute has a value of "2" for the variable representing the chemical species C, since this species appears with a stoichiometry of 2 in the chemical expression. The reversible attribute on the <reaction> element and the direction attributes on the <variable_ref> elements have their default values ("yes" and "forward", respectively) and therefore could have been omitted, but they are included for clarity.
Figure 11 A typical pathway diagram representation of the simple reversible reaction A + B <-> 2C + D.
Figure 12 The CellML definition of the simple reversible reaction A + B <-> 2C + D. See text for more details.
Figure 13 shows the pathway diagram for the following irreversible, catalyzed reaction, which exhibits product-inhibition:
A + B -> D (catalyzed by C, inhibited by D)
The CellML definition of this reaction is shown in Figure 14.
Figure 13 A typical pathway diagram representation of the irreversible reaction A + B -> D (catalyzed by C, inhibited by D).
Figure 14 The CellML definition of the irreversible reaction A + B -> D (catalyzed by C, inhibited by D). See text for more details.
The <variable_ref> element that references the variable representing the concentration of species D now contains two <role> elements, one with information about D as a product and the other with information about D as an inhibitor. In this example, D has the same stoichiometry in both roles, but this would not necessarily need to be the case.
7.4 Rules for CellML Documents
7.4.1 The <reaction> element
- Allowed use of the
<reaction>element- A
<component>element may contain any number of<reaction>elements. [ The use of multiple<reaction>elements within a single<component>element is discouraged. ] - A
<reaction>element must contain only the following elements, which may appear in any order:-
<variable_ref>elements in the CellML namespace, <RDF>elements in the RDF namespace.
<variable_ref>element for each variable representing a chemical species that participates in the reaction, and one<variable_ref>element for the variable representing the rate of the reaction. ] -
- Each
<reaction>element must contain at least one<variable_ref>element. - The
<reaction>element may define areversibleattribute.
- A
- Allowed values of the
reversibleattribute- If present, the
reversibleattribute must have a value of"yes"or"no". - If not present, the value of the
reversibleattribute defaults to"yes". [ It is recommended to always explicitly define the value of this attribute. ]
- If present, the
- Proper use of the
<reaction>element in encapsulating components[ It is often convenient to include a
<reaction>element in a component that is encapsulating several intermediate reactions (see Section 6 for more information about encapsulation). The encapsulating component represents an overall, or total, reaction, which can be represented by a<reaction>element. This total reaction is effectively qualitative because the mathematics representing the progression of the total reaction are defined in the components representing the intermediate reactions. ]- A
<reaction>element in an encapsulating component must not containdelta_variableattributes on the<role>elements or explicit mathematics defining the overall reaction rate or the changes in concentration of the species that participate in the total reaction. [ A CellML document should not define an inconsistent set of equations. This rule prevents authors inadvertently introducing explicit or implicit mathematics in an encapsulating component that duplicates or contradicts mathematics (either explicit or implicit) defined in the encapsulated components. ]
- A
7.4.2 The <variable_ref> element
- Allowed use of the
<variable_ref>element- A
<variable_ref>element must contain only the following elements, which may appear in any order:<role>elements in the CellML namespace,<RDF>elements in the RDF namespace.
- Each
<variable_ref>element must contain at least one<role>element. [ The recommended best practice is to define one<role>element for each role assumed by the chemical species represented by the referenced variable. ] - Each
<variable_ref>element must define avariableattribute.
- A
- Allowed values of the
variableattribute- The value of the
variableattribute on a<variable_ref>element within a<reaction>element must equal the value of thenameattribute on a<variable>element defined inside the current<component>element. - The value of the
variableattribute must be unique across all<variable_ref>elements contained within the parent<reaction>element. [ A variable must only be referenced once in a single reaction. ]
- The value of the
7.4.3 The <role> element
- Allowed use of the
<role>element- A
<role>element must contain only the following elements, which may appear in any order:-
<math>elements in the MathML namespace, <RDF>elements in the RDF namespace.
<role>elements are provided below, and rules for the<math>element and its children are given in Section 4. ] -
- Each
<role>element must define aroleattribute. It may also definedelta_variable,direction, andstoichiometryattributes.
- A
- Allowed values of the
roleattribute- The
roleattribute must take one of the following seven values:-
"reactant": the species represented by the referenced variable is one of the species consumed or transformed by the reaction (in the forward direction). Reactants are also often called substrates. -
"product": the species represented by the referenced variable is one of the species produced by the reaction (in the forward direction). -
"catalyst": the species represented by the referenced variable catalyzes the reaction. In biochemical pathways such a species will almost always be an enzyme and will almost always occur with astoichiometryattribute value of"1". -
"activator": the species represented by the referenced variable enhances the reaction. Activators can occur with any stoichiometry. An activator will usually be a small molecule that increases the activity of an enzyme catalyzing the reaction. However, the detailed reaction representing this activation of the enzyme may not be included in the model. Instead, the activator may be represented as directly affecting the kinetics of the catalyzed reaction. -
"inhibitor": the species represented by the referenced variable inhibits the reaction. Inhibitors can occur with any stoichiometry. An inhibitor will usually be a species that inhibits the activity of an enzyme catalyzing the reaction. However, the detailed reaction representing this inhibition of the enzyme may not be included in the model. Instead, the inhibitor may be represented as directly affecting the kinetics of the catalyzed reaction. -
"modifier": the species represented by the referenced variable modifies the reaction in some unspecified way. -
"rate": the referenced variable represents the rate of the reaction.
-
- The
- Proper use of the
roleattribute- A
<reaction>element must contain no more than one<variable_ref>element with a<role>element with aroleattribute with a value of"rate". [ There may only be one rate variable per reaction. ] - A
<variable_ref>element that contains a<role>element with aroleattribute value of"rate"must not contain other<role>elements. [ The variable assigned the"rate"role may not be assigned any other roles. ] - A
<role>element with aroleattribute value of"rate"must not definedelta_variableorstoichiometryattributes. [ Thedelta_variableandstoichiometryattributes have no meaning for a rate variable. ]
- A
- Allowed values of the
directionattribute- If present, the
directionattribute must take one of the following three values:-
"forward": the value of theroleattribute is the role of the referenced variable in the reaction when running in the "favoured" direction. The favoured direction is the one in which the the reactants are being consumed (i.e., the time-derivatives of their concentrations are negative), as defined by the kinetic rate law. -
"reverse": the value of theroleattribute is the role of the referenced variable in the reaction when running opposite to the "favoured" direction. In this direction, the reactants (as defined by the kinetic rate law) are being produced. -
"both": the value of theroleattribute is the role of the referenced variable in both directions of the reaction.
-
- If not present, the value of the
directionattribute defaults to"forward".
- If present, the
- Proper use of the
directionattribute- A
directionattribute on a<role>element that is inside a<reaction>element with areversibleattribute value of"no"must have a value of"forward". [ Only reversible reactions may occur in two directions. ] - A
directionattribute on a<role>element for which theroleattribute has a value of"rate","reactant"or"product"must have a value of"forward". [ Variables representing the reaction rate, a reactant or a product should always be labelled as such in the forward direction. To do otherwise would cause the implicit mathematics defined by thedelta_variableandstoichiometryattributes on the reactant and product variables to be erroneous. ] - Each
<role>element contained in a given<variable_ref>element must have a unique combination of values for theroleanddirectionattributes. [ Defining two<role>elements with the sameroleanddirectionattribute values would allow the definition of inconsistent stoichiometries or multiple delta variables for a single variable. Both of these situations would imply inconsistent mathematics. ]
- A
- Allowed values of the
stoichiometryattribute- If present, the value of the
stoichiometryattribute must be a real number. [ In most cases, the value will be an integer. However, a valid CellML model may use fractional stoichiometries. ]
- If present, the value of the
- Allowed values of the
delta_variableattribute- If present, the value of the
delta_variableattribute must equal thenameattribute on a<variable>element defined inside the current<component>element. - If present, the value of the
delta_variableattribute must be unique across all<role>elements contained within the parent<component>element. [ One variable cannot represent the rate of change in concentration of more than one species. The value of thedelta_variableattribute must be unique across the entire<component>element because it is legal (but not recommended) to include more than one<reaction>element in a single component. ]
- If present, the value of the
- Proper use of the
delta_variableattribute- A
delta_variableattribute must only appear on<role>elements in which theroleattribute has a value of"reactant"or"product". [ It is only in these roles that a chemical species may undergo a change in concentration. ] - A
<role>element on which adelta_variableattribute is declared must also either declare astoichiometryattribute or contain at least one<math>element in the MathML namespace. [ The combination of thedelta_variableattribute and thestoichiometryattribute implies a mathematical relationship between the variable referenced in thedelta_variableattribute and the variable assigned the role of"rate", as defined in Section 7.5.5. If thestoichiometryattribute is absent, the relationship between the variable assigned the role of"rate"and the variable named in thedelta_variableattribute must be defined using MathML. ] - A
<role>element on which thestoichiometryanddelta_variableattributes are both defined must not contain<math>elements in the MathML namespace. [ The equations in a<math>element inside a<role>element for which theroleattribute is"reactant"or"product"must relate the variable named in thedelta_variableattribute to the variable assigned the role of"rate". Such equations would contradict the relationship implied by thedelta_variableandstoichiometryattributes, as defined in Section 7.5.5. ] - If the
delta_variableandstoichiometryattributes are both declared on any single reaction participant, a<variable_ref>element must be provided for the variable that represents the reaction rate. This<variable_ref>must contain exactly one<role>element, with aroleattribute equal to"rate". [ The reverse is not true: a variable may be assigned a role of"rate"even if the"reactant"and"product"variables do not definedelta_variableattributes. In this case, the modeller may choose to provide explicit mathematics relating the"rate"variable to the change in concentration of the various chemical species. ]
- A
- Proper use of a
<math>element inside a<role>element- A
<math>element in the MathML namespace inside a<role>element must define equations that are relevant to the variable referenced by the containing<variable_ref>element, acting in the role defined by theroleattribute on the<role>element. [ The meaning of "relevant" in this context is discussed in Section 7.5.6. ]
- A
7.5 Rules for Processor Behaviour
7.5.1 Implications of the reversible attribute
If the reversible attribute on a <reaction> element has a value of "yes", it is assumed that all reactants in the forward direction are products in the reverse direction and vice versa. Similarly, all products in the forward direction are assumed to be reactants in the reverse direction and vice versa. No assumptions must be made of the species acting in other roles.
7.5.2 The absence of a stoichiometry attribute
CellML processing software must not make any assumptions if a stoichiometry attribute is not defined on a <role> element. The absence of a stoichiometry value specifically does not imply a stoichiometry of "1". Instead, it would usually mean that the stoichiometry of the reaction is unknown.
7.5.3 Chemical information implied by the stoichiometry attribute
The value of the stoichiometry attribute on a <role> element is defined to be the stoichiometry of the chemical species whose concentration is represented by the variable referenced by the containing <variable_ref> element. This stoichiometry can be used to produce the chemical expression representation of the model.
7.5.4 The absence of a delta_variable attribute
CellML processing software must not make any assumptions if a delta_variable attribute is not defined on a <role> element.
7.5.5 Math implied by the delta_variable and stoichiometry attributes
The use of the delta_variable and stoichiometry attributes on a <role> element implies the following mathematical relationship between the declared delta variable and the rate variable (where the variable representing the reaction rate will have a negative value when the reaction is proceeding in the forward direction):
- For reactants:
delta_variable = (stoichiometry)(rate) - For products:
delta_variable = -(stoichiometry)(rate)
The two reactions shown in Figure 15 are mathematically equivalent. The representation in the first reaction in Figure 15 is the recommended best practice because processing applications are not required to be able to extract the stoichiometry from an explicit MathML definition such as the one shown in the second reaction.
Explicit mathematics should only be used in cases where the implicit formulation would be inappropriate. Some examples of such cases are:
- If the stoichiometry of a reaction is unknown, but the modeller still wishes to relate the rate of change of a particular chemical species to the general reaction rate. Defining the
stoichiometryattribute implies that the stoichiometry is known to equal the value of that attribute. - If the modeller wishes to experiment with the stoichiometry of a species in different simulations using the model. (In this case, it might be easier if the stoichiometry is defined as a variable.)
- If the math implied from the recommended formulation would be incorrect, i.e., in the rare cases when a more complex function is needed to relate the change in concentration of a species to the reaction rate.
In all of these cases, it is recommended best practice to put the mathematical expression used to define the change in concentration of a species inside the <role> element contained in the <variable_ref> element referring to the variable representing the concentration of that species.
Figure 15 The top <reaction> element shows the recommended best practice for defining the change in concentration delta_A of a chemical species A with respect to the reaction rate r. The second <reaction> element shows an equivalent representation using an explicit MathML definition. Use of this formulation is not recommended. The MathML blocks defining the rate laws are omitted.
It is an error to explicitly declare mathematics that conflicts with or duplicates implied mathematics. Therefore, a modeller must not declare a stoichiometry attribute and delta_variable attribute in addition to explicit math relating the change in concentration of the referenced species to the reaction rate.
7.5.6 Meaning of mathematics in reactions
Equations defined in <math> elements in the MathML namespace inside a <role> element must be relevant to the the variable referenced by the parent <variable_ref> element, acting in the role defined by the value of the role attribute. This means that:
- If the
roleattribute value is"rate", the equations must calculate the kinetic rate law (i.e., calculate the value of the referenced variable). Intermediate calculations related to the calculation of the rate are also allowed. Conventionally, the variable representing the reaction rate will have a negative value when the reaction is proceeding in the forward direction. - If the
roleattribute value is"reactant"or"product", the equations must calculate the relationship between the general reaction rate and the rate of change of the species represented by the referenced variable (i.e., calculate the value of variable named in thedelta_variableattribute). Intermediate calculations related to the calculation of the delta variable are also allowed. - In all other cases, the equations must relate an intermediate variable used in the rate calculation to the variable referenced by the containing
<variable_ref>element. For example, it would be appropriate to calculate an effective concentration of an inhibitor or catalyst in the<role>element contained in the<variable_ref>element that references the variable representing the actual concentration of that species.
7.5.7 Resolution of inconsistencies
Duplication of information is avoided as much as possible. However, because modellers must be free to define arbitrary rate laws, it was not possible to eliminate all information duplication. For instance, CellML processing software is not expected to be able to deduce all information about a reaction from kinetic laws of arbitrary form, even though most information is in fact represented in these laws. Therefore, there is a possibility that the information in the mathematics and the information in the <reaction> element may be inconsistent.
It is anticipated that most modellers will define CellML models using some sort of processing software, which can reasonably be expected to write consistent mathematics. However, since CellML is a text-based format, modellers may also create or edit models by hand, and in doing so risk creating inconsistent models.
The following rules govern the required behaviour of CellML conformant processing software in the event that information in the explicitly and implicitly defined mathematics do not agree:
- CellML processing software may check for inconsistencies between mathematics explicitly defined using MathML and mathematics implicitly defined using the attributes on the
<role>element. If software does check, it is recommended that it notify the user if inconsistencies are detected. - If inconsistencies are found, CellML processing software must use mathematics explicitly defined using MathML when running a simulation with the model.
- CellML processing software may treat inconsistencies as it chooses when representing the model. For instance, software may ignore inconsistencies when rendering pathway diagrams or chemical expressions.
8 Metadata Framework
8.1 Introduction
Metadata is "data about data". In a CellML document, the principal data is the structure and mathematics of a biological model. Information that provides context for this data is metadata. Metadata can be included in a CellML document to facilitate searches of collections of models and model components. It provides a means for a modeller to include structured descriptive information about the model, which can help other modellers determine whether they can incorporate the model into their own work.
This section of the CellML specification presents a framework for the use of metadata in a CellML document. Methods for identifying types of metadata within that framework are recommended in the CellML Metadata Specification. The use of these methods ensures reliable extraction of metadata from CellML documents across all processors aware of CellML Metadata. The CellML Metadata specification is being developed independently of the CellML specification.
All metadata is optional. A model without any metadata is a valid CellML model. However, it is recommended that a CellML document author provide as much metadata as possible, particularly his/her name and contact information and a reference for a paper that describes the development of the model.
8.2 Basic Structure
Metadata should be embedded in a CellML document using the Resource Description Framework (RDF), the syntax of which is defined in the RDF Model and Syntax Recommendation. For interoperability, CellML processing software should make use of the methods for identifying types of metadata outlined in the CellML Metadata Specification.
Section 2.2.2 defines two metadata namespaces that CellML processing software is expected to recognise and recommended prefixes to which these namespaces should be mapped. RDF elements are placed in the RDF namespace, which should be mapped to the prefix rdf. CellML Metadata elements and attributes have their own namespace which should be mapped to the prefix cmeta.
CellML processing software is free to ignore any and all metadata. However, it is recommended that software at least display metadata. Model authors are free to develop their own RDF schema for metadata, or to store metadata in another format by using the CellML extension mechanism described in Section 2.2.3. However, doing so decreases the likelihood that CellML processing software will be able to do anything useful with the metadata in a CellML document.
Metadata is defined within an <rdf:RDF> element as shown in Figure 16. The rdf, cellml, and cmeta prefixes are used throughout this section to indicate that elements and attributes are in the RDF, CellML and CellML Metadata namespaces, respectively. The recommended best practice is to define the RDF namespace and any namespaces used by the enclosed metadata on the <rdf:RDF> element, even if these namespaces are already defined on the ancestor elements of the <rdf:RDF> element. This increases the re-usability of the RDF block. Furthermore, RDF processing software that does not recognise the CellML namespace can still parse a CellML document, extract the RDF blocks, and perhaps provide useful functionality with the information described in the RDF.
An <rdf:RDF> element typically contains one or more <rdf:Description> elements, each of which defines an rdf:about attribute. The value of the rdf:about attribute must be a valid Uniform Resource Identifier (URI). Metadata may be associated with the document it is defined in by assigning the rdf:about attribute an empty value (""). Metadata may be associated with an element in the current document by defining an attribute of type ID on that element and assigning the rdf:about attribute on the <rdf:Description> element a value equal to the value of that attribute preceded by a hash (#). An attribute must be given a type of ID in the document type declaration (DTD) or schema associated with an XML document, and its value must be unique across all attributes of type ID in a given document. The correct way to do this in a DTD is described in Section 3.3.1 of the XML 1.0 Recommendation.
As was discussed in Section 2.2.1, the name attribute that occurs on many CellML elements is not of type ID because it is not necessary that CellML identifiers be unique across a document. To facilitate the association of metadata with CellML elements, a cmeta:id attribute in the CellML Metadata namespace may be added to any CellML element. The CellML 1.1 DTD (given in Appendix A.6) declares this attribute to be of type ID for all CellML elements. This declaration prevents CellML elements from having any other attributes of type ID, including attributes in extension namespaces. The MathML 2.0 DTD defines an attribute id of type ID for all MathML elements. Extension elements may use their own attributes of type ID, or make use of cmeta:id attributes, which CellML processing software is required to treat as if it had type ID. The value of an attribute of type ID must conform to the requirements specified in the XML specification.
For interoperability, an RDF block should be stored in the element about which it contains metadata. This makes the element more re-useable. Elements in the MathML namespace are an exception to this recommendation. The MathML content of a <cellml:component> element might be extracted for use in a general MathML processor, which might not be able to handle RDF content. Therefore, metadata on MathML elements should be placed in the containing <cellml:component> element. If the RDF block contains metadata about the CellML document, it should be included in the root element of the document. Note that simply putting an RDF block inside an element is not sufficient to indicate that the metadata in the block refers to that element. The rdf:about attribute on the <rdf:Description> element must be used to indicate the resource about which the RDF block contains metadata.
8.3 Examples
Figure 16 demonstrates the use of metadata in CellML. Three RDF blocks are shown: one that provides metadata about the CellML document, one that provides metadata about the model, and one that provides metadata about a component contained in the model. Only the RDF framework elements are shown. The actual metadata is not shown here. Examples in the CellML Metadata Specification will demonstrate how to use the recommended metadata elements.
Figure 16 An example demonstrating how metadata can be embedded in a CellML document using the Resource Description Framework (RDF).
The first RDF block provides metadata about the CellML document. This is indicated by the empty value of the rdf:about attribute on the <rdf:Description> element. The second RDF block has a value of "#model01" in the rdf:about attribute on the <rdf:Description> element. This indicates that this metadata provides information about the model that is delimited by the <cellml:model> element with a cmeta:id attribute value of "model01". The final RDF block provides metadata about the membrane component. This is indicated by the rdf:about attribute with a value of "#comp01" on the <rdf:Description> element.
All three RDF blocks declare the RDF and CellML Metadata namespaces. This makes the RDF blocks portable: the information needed to interpret the RDF will be preserved even if the blocks are extracted from the CellML document.
8.4 Rules for CellML Documents
8.4.1 Proper use of the cmeta:id attribute
- A
cmeta:idattribute (where thecmetaprefix is mapped to the CellML Metadata namespace URI defined in Section 2.2.2) may be defined on any CellML element. Acmeta:idattribute may also be defined on extension elements for which no attribute of type ID is declared in the DTD, schema or language specification. [ On MathML elements, themathml:idattribute must be used. Acmeta:idattribute must specifically not be added to MathML elements because a given element may only contain one attribute of type ID. ]
8.4.2 The <rdf:RDF> element
- Allowed use of the
<rdf:RDF>element- Any CellML element may contain any number of
<rdf:RDF>elements. [ Metadata may appear on any CellML element and may be split across multiple<rdf:RDF>elements. The recommended practice is to enclose all metadata relevant to a particular resource in a single<rdf:RDF>element. In this and subsequent rules, the use of therdfprefix indicates that elements and attributes are in the RDF namespace. ] - The content of an
<rdf:RDF>element must conform to the Resource Description Framework (RDF) Model and Syntax Specification recommendation from the W3C. [ For interoperability, the abbreviated syntax defined in the RDF recommendation should be avoided. However anrdf:parseTypeattribute with a value of"Resource"can be added to non-RDF elements to create anonymous resources within an<rdf:RDF>element. ]
- Any CellML element may contain any number of
8.5 Rules for Processor Behaviour
8.5.1 Treatment of cmeta:id attributes
CellML processing software must treat any cmeta:id attributes in a CellML document (where the cmeta prefix is mapped to the CellML Metadata namespace URI defined in Section 2.2.2) as if they're of type ID. This has the following consequences for CellML documents:
- A
cmeta:idattribute must not be defined on a non-CellML element for which the DTD, schema or language specification has already declared an attribute of type ID. - The values of all
cmeta:idattributes and any other attributes of type ID in a given CellML document must be unique. - The values of all
cmeta:idattributes in a CellML document are potential targets for the values ofrdf:aboutattributes on<rdf:Description>elements.
8.5.2 General meaning of metadata
Metadata may refer to the CellML document, the CellML model, or a specific element within the CellML model. The following list documents the intended meaning of metadata on each of these resources. More detailed information can be found in the CellML Metadata Specification.
- Metadata that refers to the CellML document provides information relevant to the document as a whole, independent from the use of the document to specify a model. Examples of metadata that might appear on a CellML document are last modified date (date on which the document was last edited) and publisher (person or organization distributing the document).
- Metadata that refers to the CellML model provides information relevant to the model as a whole. For instance, the model author is the person who created the complete model, even if some of the components were taken from a shared database and have different authors.
- Metadata that refers to a specific CellML element provides information about that element only. It does not provide information about elements that are contained in the referenced element.
9 Importing Models
9.1 Introduction
The component-based architecture of CellML described in the previous sections gives modellers the ability to reuse parts of different CellML models. Often in systems biology, molecular behaviour is researched, modelled, and described in steps. One scientist will model the flux of ions across a cell membrane, for instance, limiting their study to certain variables. Others will build on the first's work, expanding the focus of the study, and so on. To reflect a realistic method of model building, a CellML modeller may choose to use the import features described below.
9.2 Basic Structure
To use the units definitions and components of an existing model, that model must be referenced within the current model using a <cellml:import> element. This element must be the child of a <cellml:model> element. The <cellml:import> element is used to locate the model from which components and units will be imported. The CellML import feature makes use of the W3C hyperlink standard, XLink, to identify the link between the current model and the model being imported. Each <cellml:import> element must have an xlink:href attribute. The xlink and cellml namespace prefixes are used throughout this section to indicate that the elements are in the XLink and CellML namespaces, respectively. The xlink:href attribute has a value equal to the Uniform Resource Identifier that identifies the location of the imported CellML model.
The <cellml:import> element may contain one or more <cellml:units> elements to declare the units that are being imported. A <cellml:units> element appearing as a child of a <cellml:import> element must have a units_ref attribute and a name attribute. The value of the units_ref attribute must equal the value of a name attribute of a <cellml:units> element in the model being referenced by the import. Units local to components may not be imported. The value of the name attribute is a unique identifier by which the component will be referenced throughout the rest of the model. The <cellml:units> element is described in detail in Section 5.
Similarly, the <cellml:import> element may contain one or more <cellml:component> elements to declare the component trees that are being imported. Component trees comprise of components and their descendants. For instance in Figure 17, the component tree of component 1 consists of components 1, 2, 3, 5, and 6. A <cellml:component> element appearing as a child of a <cellml:import> element must have a component_ref attribute and a name attribute. The value of the component_ref attribute must equal the value of a name attribute of a component in the model being referenced by the import. The value of the name attribute is a unique identifier by which the component will be referenced throughout the rest of the model. The <cellml:component> element is described in detail in Section 3.
Figure 17 The encapsulation hierarchies of two models. Blue boxes represent components, green arrows represent an 'encapsulated by' relationship, thus component 5 is encapsulated by component 2, etc.
The connections are only maintained between the components and their component trees listed in one <cellml:import> element; therefore, if an imported component relies on values from other components in the original model, every component from which it obtains values needs to be imported. However, a modeller may use separate <cellml:import> elements locating the same model to import various component trees without connections.
Any components and units from another model referenced in the current model must first be declared in the <cellml:import> element. After imported units have been declared, they can be used in the same way any other units are used within a model. Connections may be made between imported components and components defined in the current model as described in Section 3.
9.3 Examples
Figure 18 demonstrates the use of the <cellml:import> element to import parts of another CellML model located at http://www.example.com/myocyte_model.xml which contains a component with a name of "sodium_channel" and a units definition with the name of "millivolts". In this model, we'll refer to the "sodium_channel" component as "Na_channel".
In a newly defined component in the current model (the membrane component), variables may use the imported millivolts units. The membrane component sends out the membrane voltage to the imported Na_channel component and receives the resulting value for the sodium current for subsequent calculations. It is not necessary to explicitly import encapsulated components because the entire component tree will be imported along with encapsulating components.
Figure 18 The <cellml:import> identifies the URI of the model from which the components and units are being imported. See text for more details.
Figure 19 shows part of a description of the tricarboxylic acid (TCA) cycle. The modeller wants to import the resulting pyruvate concentration from the glycolysis pathway as the initial concentration of the pyruvate for the TCA cycle. Because the pyruvate concentration depends on the entire glycolysis pathway, all of the unencapsulated components from the CellML description of the glycolysis pathway need to be imported individually so that the connections between the components are maintained.
Figure 19 The modeller wants to run the end pyruvate concentration of the glycolysis pathway through the TCA cycle. In order to do this, the model description of the TCA cycle (the current model) must import all of the unencapsulated components in the model description of the glycolysis pathway because the pyruvate concentration depends on the entire glycolysis pathway.
9.4 Rules for CellML Documents
9.4.1 The <import> element
- Allowed use of the
<import>element- A
<cellml:import>element must contain only the following elements, which may appear in any order:<component>and<units>elements in the CellML namespace,<RDF>elements in the RDF namespace.
- Each
<cellml:import>element must define anxlink:hrefattribute. [ In this and subsequent rules, thecellmlandxlinkprefixes are used to indicate that elements and attributes are in the CellML and XLink namespaces, respectively. ]
- A
- Proper use of the
<cellml:import>element- A model must not import a model that directly or indirectly imports itself. [ The model tree must be acyclic. ]
- A model must not import a units definition that is local to a component.
- Allowed values of the
xlink:hrefattribute- The value of the
xlink:hrefattribute must be a valid Uniform Resource Identifier.
- The value of the
9.5 Rules for Processor Behaviour
9.5.1 Treatment of imported units
- Imported units become named instances in the current model. [ Imported units are treated as templates from which to create instances in the current model. ]
- When the imported units are used, the units must be resolved from the source model. [ An imported units definition may depend on other units defined in the source model. ]
9.5.2 Treatment of imported components
- Imported components become named instances in the current model. [ Imported components are treated as templates from which to create instances in the current model. ]
- For each
<cellml:import>element in the current model, CellML processing software must include each CellML component listed and the connections between them. - An imported component must represent an instance of its component subtree from the model being referenced by the
<cellml:import>element. [ An imported component may depend on components it encapsulates in the source model. ] - Units used in an imported component must be resolved from the source model. [ An imported component may depend on units defined in the source model. ]
A Using The CellML 1.1 DTD
A.1 Introduction
This section contains some recommendations on the use and referencing of the CellML 1.1 DTD, the full text of which is given in Appendix A.6. The document rules and processor behaviour described in this section are not required in valid CellML documents and from CellML conformant processing software, respectively.
A.2 The CellML DOCTYPE Declaration
CellML documents may reference the version of the CellML 1.1 DTD maintained on the CellML website with a DOCTYPE declaration of the following form:
"model" may be changed to match the root element of the CellML document.
CellML document authors may change the value of the system identifier to point to a copy of the DTD cached on a local filesystem if this is available. This specification does not define a public identifier for CellML 1.1. For interoperability, CellML document authors should not define one unless specifically needed for a parser that makes use of SGML catalog files.
A.3 CellML without a DTD
CellML documents are not required to contain a DOCTYPE declaration. In the absence of a DTD, CellML processing software needs to take into account the following important points:
- All
cmeta:idattributes are of type ID. - All
idattributes on MathML elements are of type ID.
The CellML DTD does not define the default values for CellML attributes that are defined in the specification. With or without a DTD, CellML processing software is responsible for setting these values, if not specified.
A.4 Use of MathML within CellML
The CellML 1.1 DTD can be used in conjunction with the MathML 2.0 DTD to validate any MathML content within a CellML document. The CellML DTD contains a reference to the MathML 2.0 DTD, which is maintained at the World Wide Web Consortium's website, inside a conditional section, which by default is not included in the CellML DTD. CellML document authors may cause the conditional section to be included by setting the value of the "use_mathml_dtd" entity to "INCLUDE" inside the internal subset of their CellML document, as shown below:
If copies of both the CellML 1.1 DTD and the MathML 2.0 DTD are available on the local filesystem, it is possible to conveniently override the reference to the MathML 2.0 DTD by setting the value of the "mathml_dtd_path" entity to the appropriate relative path from the CellML DTD to the MathML DTD, as shown below:
The MathML 2.0 DTD is not on the CellML website, so DOCTYPE declarations of this form will fail when referencing the DTD on the CellML website. The MathML 2.0 DTDs are available as a ZIP archive, a link to which is given in Appendix A.6 of the MathML 2.0 Recommendation.
The CellML specification requires a cellml:units attribute to be defined on all <mathml:cn> elements (where the cellml and mathml prefixes are mapped to the URIs for the CellML and MathML namespaces, respectively). For this reason, the conditional section of the CellML DTD in which the MathML DTD is referenced also redeclares the list of attributes on the <mathml:cn> element to include the cellml:units attribute. This will prevent XML parsers from finding errors when validating valid CellML documents against the MathML DTD.
A.5 Treatment of Namespaces
In Section 2.2.2, it was suggested that the root element of a CellML document set the default namespace and map the cellml prefix to the CellML namespace URI. Use of unprefixed element names (i.e., default namespaces) is encouraged to ensure DTD-based validation will work correctly. The CellML 1.1 DTD defines three optional attributes on every CellML element that can be used to set namespaces where necessary. These are xmlns, xmlns:cellml and xmlns:cmeta.
A.6 The CellML 1.1 DTD
The CellML 1.1 DTD is available at the following URI:
The CellML 1.1 DTD does not attempt to declare or reference declarations for the metadata framework elements in the RDF namespace. It also doesn't declare the default values of any of the attributes on the CellML elements.
For convenient reference, the text of the DTD is given below.
B Scripting Functionality in CellML
B.1 Introduction
MathML can be extended by defining new operators, the behaviour of which is not defined in MathML. These operators could be used to call functions implemented in software (i.e., implicitly) or defined using a scripting language (i.e., explicitly). CellML 1.1 does not require processing software to implement support for scripting functionality. This section contains some recommendations on best practices for adding scripting functionality to CellML.
For the purposes of this discussion, it is assumed that scripting functionality will be implemented via function calls. Software that extends the functionality of MathML in other ways should extrapolate these recommendations as appropriate.
B.2 Availability of Scripts
Functions referenced in a CellML document that are defined using non-MathML syntax should be identified by, and accessible via, a URI. A function could, for instance, be accessible via HTTP from a database using a CGI script that takes an SQL expression as an argument.
B.3 Embedding Scripts in CellML
Functions should be defined within elements in an application-specific extension namespace, if the functions are embedded within CellML documents. If the embedded script is only referenced by a single component, the script should be defined within the corresponding <cellml:component> element. If the embedded script is referenced by more than one component, the script should be defined within the <cellml:model> element.
B.4 Preferred Scripting Language
Implementors considering adding scripting functionality to CellML processing software are encouraged to use ECMAScript. It is anticipated that, if scripting functionality is officially endorsed by a future version of CellML, ECMAScript will be the scripting language that processing software is required to implement. ECMAScript is the recommended language because it is simple, standardised, and open source interpreting libraries are freely available.
ECMA is an international industry association that develops standards in information and communication for the European union. ECMA took the scripting language that Netscape developed for adding interactive content to its web browser and developed the formal language specification ECMA-262 (ECMAScript Language Specification).
B.5 Referencing Scripts from MathML
The MathML 2.0 Recommendation defines a <mathml:csymbol> element for referencing mathematical symbols and constructs that are not defined by MathML. This element should be used for referencing functions defined using non-MathML syntax from within blocks of MathML. Processing software should take into account the following recommendations regarding the use of the <mathml:csymbol> element for this purpose.
B.5.1 The <mathml:csymbol> element
- Recommended use of the
<mathml:csymbol>element- The
<mathml:csymbol>element should only appear as the first child element within a<mathml:apply>element. [ A<mathml:csymbol>element should only be used as an operator, which is "applied" to some arguments. ] - After leading and trailing whitespace is removed, the content of a
<mathml:csymbol>element must be a valid CellML identifier as discussed in Section 2.2.1. This identifier must accurately represent the external function referenced. [ The content of a<mathml:csymbol>element should preferably be a human-readable identifier for the external function. If the function is defined using a common scripting or programming language, then this identifier should be the name of the function. ] - Each
<mathml:csymbol>element should define adefinitionURLand anencodingattribute.
- The
- Recommended use of the
mathml:definitionURLattribute- The value of the
definitionURLattribute should be a valid URI that identifies a single resource containing the definition of the external function.
- The value of the
- Recommended use of the
mathml:encodingattribute- The value of the
encodingattribute should indicate to processing software the format of the externally defined function. [ In the version of CellML that describes how external functions are to be defined within the CellML framework, theencodingattribute will be moved into the CellML namespace and will be required to take a value from a controlled vocabulary. ]
- The value of the
B.6 Effects of Scripts
Functions must be side-effect free. That is, a function must not assign values to variables that are not local to that function. In particular, functions must not alter the values of their arguments or global variables.
C Advanced Units Functionality
C.1 Introduction
CellML 1.1 lays the foundations of a flexible and robust system for the association of units with variables and constants in cellular models. However, it does not require software to make use of the units information contained in CellML documents. This section presents algorithms and examples demonstrating some of the advanced features related to units that CellML processing software might choose to offer modellers. For interoperability, CellML processing software that includes these features should achieve the same results as the algorithms described here, although the exact implementation may differ.
C.2 Terminology
C.2.1 Equivalence of units references
Two units references are considered equivalent if they satisfy one of the following criteria:
- They reference the same units definition from the standard dictionary.
- They reference the same units definition in the current
<component>element. - They reference the same units definition in the current
<model>element, where that units definition is not superseded by a units definition with the same name in the current<component>element.
C.2.2 Dimensional equivalence of units definitions
Two units definitions have dimensional equivalence if, when each is recursively expanded and simplified until left with nothing but products of SI and user-defined base units:
- the expanded form of each units definition consists of the same set of base units, and
- the exponent on each base unit is identical in each expanded units definition.
Algorithms for the expansion and simplification of units definitions are given in Appendix C.3.4 and Appendix C.3.1, respectively.
C.3 Algorithms
C.3.1 Simplification of units definitions
It is frequently convenient to be able to simplify a units definition, where this units definition is the result of the application of some mathematical operator to terms which have units associated with them. These operators include the <times>, <divide> and <diff> operators.
The simplification of a units definition is an iterative process in which the number of other units definitions referenced is systematically reduced. References to units definitions may be removed in the following cases:
- If two units references are equivalent (as defined in Appendix C.2.1) and have exponents with equal and opposite value, then they may be replaced by a reference to
dimensionless. - If two units references are equivalent (as defined in Appendix C.2.1) then they may be replaced with a single units reference to the same units, where the exponent associated with that units reference is the sum of the exponents on the original two units references.
- If a units definition references
dimensionlessone or more times in addition to some other units, any references todimensionlessmay be removed. - If a units definition references
dimensionlessone or more times and references no other units, the definition may be replaced withdimensionless.
The above rules only allow the removal of units references that are equivalent as defined in Appendix C.2.1. This scheme would not allow references to identical units definitions in two different components to be cancelled and removed, because the references would not satisfy the equivalence criteria.
C.3.2 Units-based restrictions on the use of MathML operators
This section describes restrictions on the units associated with a collection of terms to which each MathML operator in the CellML set (defined in Section 4.2.3) can be applied. For instance, the <mathml:plus> operator can only be applied to terms that have dimensionally equivalent units. The restrictions invalidate the application of certain MathML operators to certain collections of terms based on their units, and are used in equation dimension checking, as described in Appendix C.3.6.
The restrictions are given in Table 5. The <mathml:root>, <mathml:diff> and <mathml:log> elements all take qualifiers, in addition to operands.
| Operator | Restrictions |
|---|---|
<times>, <divide>, <abs>, <floor>, <ceiling> |
There are no restrictions on the units of operands for these operators. |
<eq>, <neq>, <gt>, <lt>, <geq>, <leq>, <plus>, <minus> |
These operators, if applied to more than one operand, require all of their operands to have either equivalent units references, as defined in Appendix C.2.1, or to reference units that have dimensional equivalence, as defined in Appendix C.2.2. |
<and>, <or>, <xor>, <not> |
These operators require their operands to have units of cellml:boolean, as defined in Section 5.5.2. |
<exp>, <ln>, <factorial>, <sin>, <cos>, <tan>, <sec>, <csc>, <cot>, <sinh>, <cosh>, <tanh>, <sech>, <csch>, <coth>, <arcsin>, <arccos>, <arctan>, <arccosh>, <arccot>, <arccoth>, <arccsc>, <arccsch>, <arcsec>, <arcsech>, <arcsinh>, <arctanh> |
These operators require their operands to have units of dimensionless. |
<power> |
This is a binary arithmetic operator. Its first operand may have any units, and its second operand must have units of dimensionless. |
<root> |
This is a qualified unary operator. Its operand may have any units. The value of the <degree> qualifier element, if present, must have units of dimensionless. |
<log> |
This is a qualified unary operator. Its operand must have units of dimensionless. The value of the <logbase> qualifier element, if present, must have units of dimensionless. |
<diff> |
The operand of this operator and the value of the <bvar> qualifier element, if present, may have any units. The value of a <degree> qualifier element within the <bvar> qualifier element, if present, must have units of dimensionless. |
Table 5 The restrictions on the units associated with operands and qualifiers for each MathML operator. All elements in this table are in the MathML namespace.
C.3.3 Applying operators to units definitions
This section defines the units resulting from the application of MathML operators to a collection of terms, each with known units. This is needed for units definition conversion and equation dimension checking, as described in Appendix C.3.5 and Appendix C.3.6, respectively. The units on each of the terms in the collection must satisfy the restrictions defined in Appendix C.3.2 for the current operator.
The full set of units calculation rules are described in Table 6.
| Operator | Result Units |
|---|---|
<eq>, <neq>, <gt>, <lt>, <geq>, <leq>, <and>, <or>, <xor>, <not> |
The result of these operators has units of cellml:boolean. |
<exp>, <ln>, <log>, <factorial>, <sin>, <cos>, <tan>, <sec>, <csc>, <cot>, <sinh>, <cosh>, <tanh>, <sech>, <csch>, <coth>, <arcsin>, <arccos>, <arctan>, <arccosh>, <arccot>, <arccoth>, <arccsc>, <arccsch>, <arcsec>, <arcsech>, <arcsinh>, <arctanh> |
The result of these operators has units of dimensionless. |
<plus>, <minus>, <abs>, <floor>, <ceiling> |
The result of these operators has the same units as the operands. |
<times> |
The result of this operator has units that are the product of the units on the operands. This product may be simplified according to the rules outlined in Appendix C.3.1. |
<divide> |
The result of this operator has units that are the quotient of the units on the first and second operands. This quotient may be simplified according to the rules outlined in Appendix C.3.1. |
<power> |
The result of this operator has units that are the units on the first operand raised to the power of the second operand. If the first operand has units of dimensionless, the result also has units of dimensionless. |
<root> |
The result of this operator has units that are the units on the first operand raised to one over the value of the <degree> qualifier element (the default value of which is 2.0). If the first operand has units of dimensionless, the result also has units of dimensionless. |
<diff> |
The result of this operator has units that are the quotient of the units of the operand over the units of the term in the <bvar> qualifier element raised to the value of the <degree> qualifier element inside the <bvar> qualifier element (the default value of which is 1.0). This quotient may be simplified according to the rules outlined in Appendix C.3.1. |
Table 6 The units of the result after applying each MathML operator to a collection of terms, where the units on those terms satisfy the restrictions in Appendix C.3.2. All elements in this table are in the MathML namespace.
C.3.4 Expansion of units definitions
This section presents the recommended algorithm for expanding a given units definition into an expression that relates the defined units to only SI and user-defined base units. This algorithm may be used in the conversion of units definitions and equation dimension checking, algorithms for which are defined in Appendix C.3.5 and Appendix C.3.6, respectively. Examples of the expansion of units definitions are given in Appendix C.4.2.
The specific steps in the algorithm depend on whether the units definition to be expanded is simple or complex, as defined in Section 5.2.2. Both derivations use recursive methods. At each step, any units that are not base units are replaced with expansions based on the appropriate definition.
Expansion of simple units definitions
The formula relating a variable xU with units of U (where U are simple units), to a variable x1 with units of u1 (the subunits referenced by the units attribute on the <unit> element inside the units definition for U), is given in Equation 9. This is based on the simple units definition formula given in Equation 3.
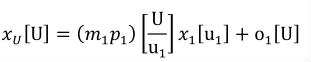 |
(9) |
m1, p1 and o1 correspond to the multiplier, prefix and offset attributes on the <unit> element, respectively.
The formula relating a variable with units of u1 to its subunits u2, as referenced in the units definition for u1, is given in Equation 10.
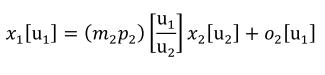 |
(10) |
Equation 10 can be substituted into Equation 9 to give Equation 11.
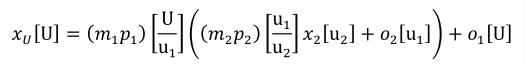 |
(11) |
The expression defining each new set of units in terms of its subunits can be substituted into the current expression recursively until an expression is reached that relates xU to xn with units un, which are SI or user-defined base units. At this point expansion stops, and the resulting expression can be simplified. This simplification combines multiplier, prefix and offset terms and combines their units based on the rules defined in Appendix C.3.3. The result is an expression of the form given in Equation 12.
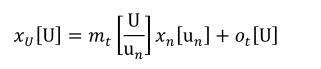 |
(12) |
The values of mt and ot are given by Equation 13 and Equation 14, respectively.
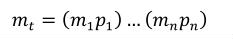 |
(13) |
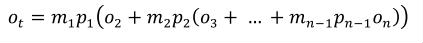 |
(14) |
Expansion of complex units definitions
The formula relating a variable xU with complex units U to a variable xA with units that are the product of the subunits referenced in the units definition for U is given in Equation 15. This is based on the complex units definition formula given in Equation 4.
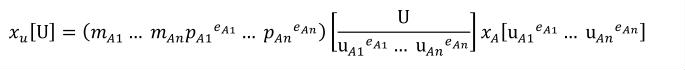 |
(15) |
The mAi, pAi, uAi and eAi refer to the values of the multiplier, prefix, units and exponent attributes on the i-th <unit> element inside the units definition for U, respectively. If, at the first step, the c-th set of units referenced is not SI or user-defined base units, the formula relating uAc to the c-th set of units referenced to its subunits is given in Equation 16.
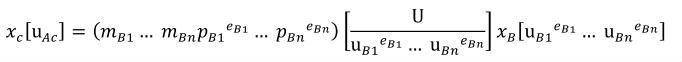 |
(16) |
Note that if uAc is a simple units definition, then the right hand side of Equation 16 will take the form of a simple units definition, but without the constant offset term.
An expansion for xA that incorporates the expansion for uAc is obtained by multiplying both sides of Equation 16 by unitary coefficients with units of the product of all of the units referenced on the right hand side of Equation 15 with the exception of uAc. Expansion of units definitions involves constructing expansions for the variable on the right hand side. The expansion continues recursively as long as any of the units on the right hand side of Equation 15 are not SI or user-defined base units. The resulting expansion can be simplified by combining multiplier and prefix terms to give an expression with the form given in Equation 17.
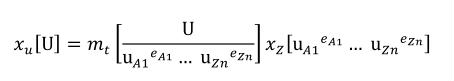 |
(17) |
uIi corresponds to the units referenced by the i-th units definition referenced in the I-th definition to be expanded, and mt is given by Equation 18.
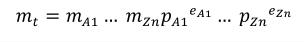 |
(18) |
mIi, pIi and eIi correspond to the values of the multiplier, prefix and exponent attributes on the i-th <unit> element in the I-th definition to be expanded.
C.3.5 Conversion between units definitions
This section presents an algorithm that specifies a possible method for converting a variable's value from one set of units to another. An example demonstrating the use of this algorithm is given in Appendix C.4.3.
If the two variable declarations that are to be mapped both reference equivalent units definitions as defined in Appendix C.2.1, then there is a one-to-one mapping between the variable's value in both components.
If the two variable declarations that are to be mapped reference different units definitions, then software may choose to calculate a conversion formula as follows. Given a variable x with units Ux, the value of which is to be passed to a variable y with units Uy, the following steps should be followed:
-
The units definitions for
UxandUyare fully expanded and simplified according to the algorithm presented in Appendix C.3.4. This yields expressions for x and y in terms of xn and yn, the units of which are products of only SI and user-defined base units. The expression for x will be of the form given in Equation 19 ifUxis a simple units definition, or of the form given in Equation 20 ifUxis a complex units definition.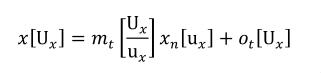
(19) 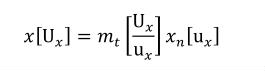
(20) In Equation 19,
uxcorresponds to the base units referenced in the full expansion ofUx, whereas in Equation 20,uxcorresponds to the product of all of the base units in the full expansion raised to the appropriate exponents. -
It should be considered an error if the units for xn (
ux) and yn (uy) do not have equivalent dimensions as defined in Appendix C.2.2. -
The expansion of x is inverted to give an expression for xn. The inverted forms of Equation 19 and Equation 20 are given in Equation 21 and Equation 22, respectively.
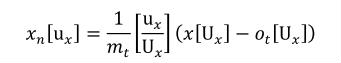
(21) 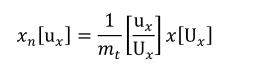
(22) The appropriate expression for xn can then be substituted for yn in the expansion of y. This yields an equation for y in terms of x, which can be used to convert variable values.
C.3.6 Equation dimension checking
This section presents an algorithm that can be used to verify that an equation is consistent with respect to the dimensions of the units definitions referenced by all numbers and variables. An example that demonstrates the process of equation dimension checking for an equation defined in MathML and CellML is given in Appendix C.4.4.
This algorithm relies on the restrictions and behaviour of the different operators with respect to units defined in Appendix C.3.2 and Appendix C.3.3. Future versions of the specification may extend this algorithm to handle other operators. The steps in the algorithm are:
-
The equation is split into a tree of terms, in which each parent term is obtained by the application of a single operator to its children. The root of the tree is the entire equation, which is created by applying a relational operator (typically the equals operator) to its child terms. All other terms in the tree are created by applying arithmetic operators to child terms.
-
The units definitions for the terms at the leaves of the tree (which will be variables, numbers, or MathML constants elements) are expanded into functions of the SI and user-defined base units, using the algorithm presented in Appendix C.3.4.
-
Starting at the leaves of the tree, sets of child terms are recursively removed from the tree and units assigned to the parent terms. The removal of each set of terms follows the following steps:
-
The child terms are compared against the restrictions described in Appendix C.3.2 for the current operator. It should be considered an error if they do not satisfy these restrictions, in which case the equation has inconsistent dimensions.
-
Units are assigned to the parent term as defined in Appendix C.3.3 for the current operator.
-
- The equation has self-consistent dimensions if no inconsistencies were found during the recursive removal of child terms during the traversal from leaves to root.
C.4 Examples
C.4.1 User-defined units and new base units
In Figure 20, the example units definitions given in Section 5.3 are reproduced. These examples are used in the subsequent advanced examples.
Figure 20 Some examples of the use of the <units> element demonstrating the definition of simple and complex units.
C.4.2 Expansion of user-defined units
In this section, the expansion of user-defined units according to the algorithm described in Appendix C.3.4 is demonstrated for each of the units definitions given in Figure 20.
The first <units> element in Figure 20 defines units named pH, and defines a base_units attribute with a value of "yes". This indicates that it should be treated by processing software as if it were an SI base unit, and that it cannot be expanded.
The definition of inch in Figure 20 is a simple units definition as it references only a single unit with an exponent of one. When the appropriate terms are substituted into Equation 3, the conversion from metre to inch is given by Equation 23. metre is a SI base unit, so no further expansion is necessary.
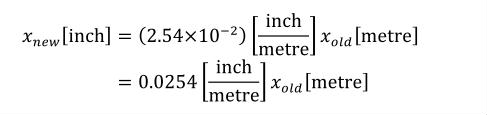 |
(23) |
The definition of fahrenheit is in terms of celsius, which is an SI derived unit. The expansion from celsius to kelvin, an SI base unit, is obtained from Section 2.1.1.5 of the SI standard, and is given in Equation 24.
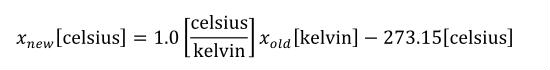 |
(24) |
The first step in the expansion of the fahrenheit definition is given in Equation 25.
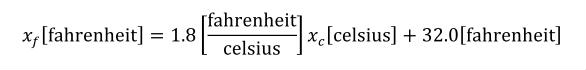 |
(25) |
The xc term can be replaced with the expansion of the celsius definition from Equation 24, as shown in Equation 26.
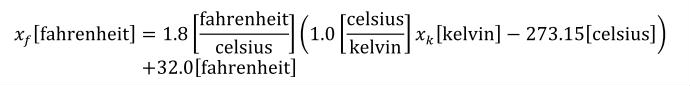 |
(26) |
The 1.0 and 273.15 terms can be multiplied by the 1.8. The units on the resulting terms are the products of the units on the operands, as described in Appendix C.3.3, and these can be simplified according to the rules given in Appendix C.3.1. The final expansion of fahrenheit is given in Equation 27
 |
(27) |
celsius_per_centimetre is the first of the complex units definitions given in Figure 20. The first step in the expansion of this definition is given by Equation 28, which is obtained by substituting the appropriate terms in Equation 4.
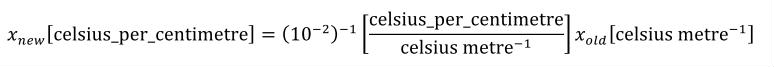 |
(28) |
The expansion of the xold term, which has units that are a product, is not obvious. This term must be expanded to continue. metre is an SI base unit, so need not be expanded. However, celsius is an SI derived unit, the expansion of which is given in Equation 24. Because this expansion is to be substituted into a complex units definition, the offset term is dropped. The next step in the expansion makes use of the modified celsius definition in Equation 29 and the identity in Equation 30.
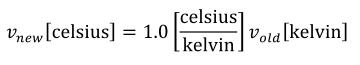 |
(29) |
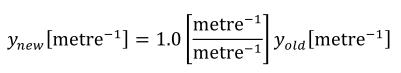 |
(30) |
The result of multiplying Equation 30 and Equation 29 is given in Equation 31.
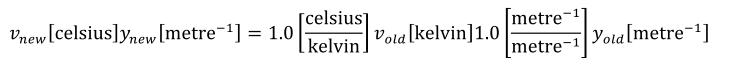 |
(31) |
The vnew and ynew variables can be multiplied together to produce a new unknown znew which has units which are the product of the units on vnew and ynew. Similarly zold is the product of vold and yold. The result is given in Equation 32, where the scale factors have also been multiplied.
 |
(32) |
znew from Equation 32 can be substituted in place of Equation 28, and the result simplified to give the complete expansion of celsius_per_centimetre shown in Equation 33.
 |
(33) |
The definition of fahrenheit_per_inch can be handled in the same way. The first step in the expansion is given by Equation 34.
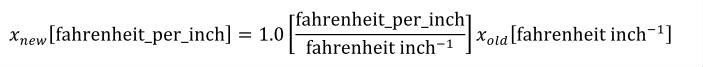 |
(34) |
The expansion of xold requires the removal of the offset from the expansion of fahrenheit from Equation 27 and the inversion of the expansion of inch from Equation 23. These are given in Equation 35 and Equation 36, respectively.
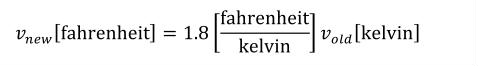 |
(35) |
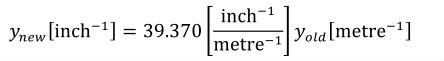 |
(36) |
Multiplying Equation 35 and Equation 36 and simplifying yields Equation 37.
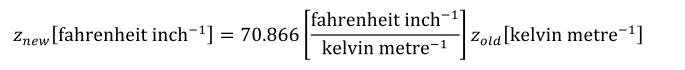 |
(37) |
znew from Equation 37 can be substituted into Equation 34 in place of xold and the result simplified to give the complete expansion of fahrenheit_per_inch in Equation 38.
 |
(38) |
The first step in the expansion of pH_per_celsius is given in Equation 39.
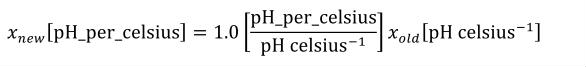 |
(39) |
When user-defined base units are referenced in a simple or complex units definition, they are treated in the same way as SI base units, and not expanded. The final expansion into a combination of user-defined and SI base units is given in Equation 40.
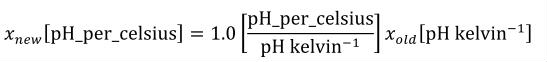 |
(40) |
C.4.3 Conversion between units definitions
In this section, the algorithm defined in Appendix C.3.5 for converting a variable's value from one set of units to another is presented with respect to a practical example. Figure 21 contains part of a CellML model definition, consisting of two components and one connection. The legacy_imperial component defines a variable x with units of fahrenheit_per_inch. The modern_si component defines a variable y with units of celsius_per_centimetre. A connection between the two components maps x to y.
Figure 21 In this model fragment, a connection maps a variable x with units of fahrenheit_per_inch to a variable y with units of celsius_per_centimetre.
The CellML definitions of both fahrenheit_per_inch and celsius_per_centimetre are given in Figure 20. It was shown how to obtain expressions that relate each of these units definitions to the SI base units in Appendix C.4.2. These expressions are reproduced in Equation 41 and Equation 42, respectively.
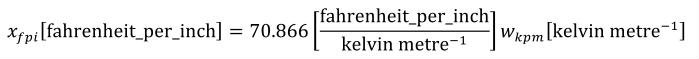 |
(41) |
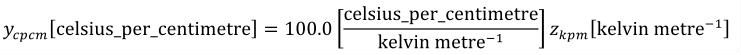 |
(42) |
The value of x is transferred to the variable y in the mapping. Therefore an equation expressing celsius_per_centimetre in terms of fahrenheit_per_inch is needed. This can be obtained by rearranging Equation 41 for wkpm, substituting the resulting expression in place of zkpm in Equation 42, and simplifying the result according to the rules defined in Appendix C.3.1. This gives the expression in Equation 43.
 |
(43) |
C.4.4 Equation dimension checking
In this section, the algorithm defined in Appendix C.3.6 for checking that an equation has consistent units is presented with respect to a practical example. Figure 22 contains the definition of a CellML component sodium_channel_m_gate. This component defines three sets of units (per_millisecond, millivolt, and per_millivolt), two variables (V and alpha_m) and an equation that calculates the value of alpha_m.
Figure 22 Parts of the CellML definition of the Hodgkin Huxley squid axon model. The sodium_channel_m_gate component defines three sets of units, two variables V and alpha_m, and the calculation of alpha_m.
Equation 44 gives the equation in Figure 22, where units have been omitted. Equation 45 gives the same equation, with the units associated with each number and variable are included. The first 1.0 in the equation is included specifically for units consistency. It would be possible to associate more complex units with the 0.1 in the numerator of the equation, but this would not accurately reflect the intent of the original model authors. CellML processing software is free to find this and similar terms that do not affect the mathematics and ignore them when interpreting the equation.
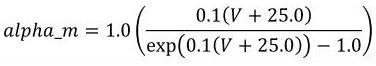 |
(44) |
 |
(45) |
The first step in the algorithm proposed in Appendix C.3.6 for verifying that a given equation has consistent dimensions is to convert the equation into a tree of equation parts. Equation 45 can be broken up into the tree shown in Figure 23.
Figure 23 The tree form of Equation 45, in which each non-leaf node is obtained by the application of a single operator to its children. Each operator is represented by a number in square brackets. The effect of each operator is discussed in the text.
At each branch in the tree, a single operator is applied to the child nodes, combining them into a larger parent equation part. Each equation part in the tree has units associated with it. In the case of leaf nodes, these units are obtained from the MathML equation definition. Parent nodes have units defined by the operator and the units on their child nodes, as described in Appendix C.3.3. Dimension checking begins at the leaf nodes, which are recursively removed as the units are evaluated for their parent nodes, which in turn become leaf nodes, as described in Appendix C.3.6.
In the equation tree diagram in Figure 23, the application of each operator to a set of child nodes is denoted by a number in square brackets, where the number reflects the order in which the operations are processed. These operations are discussed below.
- The
<plus>operator combines the variable "V" and the number "25.0" that occur in the denominator of the fraction in Equation 45. The<plus>operator requires all of its operands to be dimensionally equivalent, as described in Appendix C.2.2. The resulting equation part will have the same units as the operands. Both "V" and "25.0" have units ofmillivolt, and so the parent equation part "V +25.0" also has units ofmillivolt. - The
<times>operator (which is not explicitly rendered in Equation 45) multiplies the "V +25.0" term that is the result of the first operation by the number "0.1" which has units ofper_millivolt. The<times>operator can be applied to any operands, independent of their units, and the resulting equation part has units that are the product of the units on the operands. In this case, the resultant "0.1(V +25.0)" term has units that are the product ofmillivoltandper_millivolt, which simplifies todimensionless(as described in Appendix C.3.1). - The
<exp>operator is a unary arithmetic operator and its operand must have units ofdimensionless. The result of applying the operator, in this case "exp(0.1(V +25.0))", also has units ofdimensionless. - The
<minus>operator subtracts the number "1.0", which has units ofdimensionless, from the term resulting from operation 3. The<minus>operator requires both its operands to have the same units and the result assumes those units. - The
<plus>operator is applied to the variable "V" and the number "25.0" from the numerator of the fraction in Equation 45. Units are handled as in operation 1. - Exactly as in operation 2, where the operands are now in the numerator of the fraction in Equation 45.
- The
<divide>operator is applied to the results of operations 6 and 4, which both have units ofdimensionless. The<divide>operator can be applied to any operands, independent of their units, and the result has the quotient of the units on the operands. In this case, the resulting fraction has units ofdimensionless. - The
<times>operator is applied to the number "1.0", which has units ofper_millisecondand the result of operation 7, which has units ofdimensionless. The resulting term has units ofper_millisecond. - Finally, the
<equals>operator is applied to the variable "alpha_m" and the term resulting from operation 8. The<equals>operator requires that its operands have dimensionally equivalent units.
D Changes
D.1 Changes between the 6 November 2002 Draft and the 30 September 2003 Draft
Editorial Changes
- Specification Wide
- Several minor editorial changes have been made to all sections of the specification.
Changes to the Language
- Specification Wide
- The
<import_model>element was changed to the<import>element.
- The
- Section 3.2.2: Definition of components
- Added the
component_refattribute. - Added description about how
<component>element depends on its context.
- Added the
- Section 3.2.3: Definition of variables
- Removed description of the
units_modelattribute.
- Removed description of the
- Section 3.2.4: Definition of connections
- Removed description of the
model_1andmodel_2attributes.
- Removed description of the
- Section 3.4.2: The
<component>element- Added rules about the
component_refattribute. - Added context-based rules.
- Added rules about the
- Section 3.4.3: The
<variable>element- Removed the
units_modelattribute.
- Removed the
- Section 3.4.5: The
<map_components>element- Removed all references to the
model_1andmodel_2attributes.
- Removed all references to the
- Section 5.2.2: User defined units
- Removed the
units_modelattribute. - Added the
units_refattribute. - Added description about how
<units>element depends on its context.
- Removed the
- Section 5.4.1: The
<units>element- Added rules about the
units_refattribute. - Added context-based rules.
- Added rules about the
- Section 5.4.2: The
<unit>element- Removed the
units_modelattribute.
- Removed the
- Section 9: Import Model
- This entire section has been re-written because the ideas behind the import feature have changed drastically. Instead of importing the entire model, the modeller now has a choice in the parts of the model that are imported.
- The
xlink:titleattribute is no longer in use.
D.2 Changes between the 10 August 2001 Recommendation and the 6 November 2002 Draft
The full list of changes made between the 10 August 2001 Recommendation of the CellML 1.0 specification and the 6 November 2002 Draft of the CellML 1.1 specification can be found at Appendix D of the 6 November 2002 Draft.
D.3 Changes between 18 May 2001 Final Draft and the 10 August 2001 Recommendation
The full list of changes made between the 18 May 2001 Final Draft and the 10 August 2001 Recommendation of the CellML 1.0 specification can be found at Appendix D of the 10 August 2001 Recommendation.
D.4 Changes between 2 March 2001 Draft and the 18 May 2001 Final Draft
The complete list of changes made between the 2 March 2001 Draft and the 18 May 2001 Final Draft of the CellML 1.0 specification can be found at Appendix D of the 18 May 2001 Final Draft.

